 |
A P. 4972. feladat (2017. november) |
P. 4972. Egy \(\displaystyle \ell\) hosszúságú, könnyű és nyújthatatlan fonál egyik végét felfüggesztjük, a másikat pedig egy kicsiny gyűrűhöz kötjük, amely súrlódásmentesen csúszhat egy – a felfüggesztési pont felett \(\displaystyle d<\ell\) magasságban található – vízszintes rúdon. Az ily módon elhelyezett fonálra kifeszített állapotban egy kicsiny csiga közvetítésével \(\displaystyle m\) tömegű súlyt akasztunk a rúd közvetlen közelében, majd a rendszert magára hagyjuk.
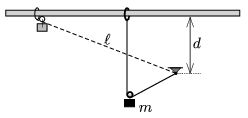
\(\displaystyle a)\) Mekkora lesz a test sebessége a pálya legalsó pontjában?
\(\displaystyle b)\) Milyen görbe mentén mozog a súly?
\(\displaystyle c)\) Mekkora erő feszíti a fonalat a pálya legalsó pontjánál?
Közli: Németh Róbert,
Budapesti Fazekas M. Gyak. Ált. Isk. és Gimn.
(5 pont)
A beküldési határidő 2017. december 11-én LEJÁRT.
Megoldás. \(\displaystyle a)\) Amikor az \(\displaystyle m\) tömegű test a pályájának legmélyebb pontjánál van, akkor mindkét fonálszál függőleges, és a csiga \(\displaystyle \tfrac12(\ell+d)\) távolságra kerül a rúdtól. Az energiamegmaradás tétele szerint a test sebessége ekkor
\(\displaystyle v=\sqrt{g(\ell+d)}.\)
\(\displaystyle b)\) A mozgás során a fonál egyik része mindvégig függőleges. (Ha nem így lenne, akkor vízszintes irányú erőt is kifejtene a gyűrűre, és az a kicsiny tömege miatt nagyon nagy gyorsulással mozogna.)
Vegyünk fel a rúddal párhuzamosan, a rúd alatt, attól \(\displaystyle \ell\) távolságban egy segédegyenest, az ábrán látható módon. Mozgása során a csiga mindig ugyanolyan messze lesz ettől az egyenestől, mint amilyen távol van az \(\displaystyle F\) ponttól, a fonál rögzített végpontjától.
Ezek szerint a pályagörbe parabola, melynek fókuszpontja \(\displaystyle F\), fókusztávolsága
\(\displaystyle f=\frac{\ell-d}{2}.\)
\(\displaystyle c)\) Ha a pálya legalsó, \(\displaystyle P\)-vel jelölt pontjában a fonalat feszítő erő \(\displaystyle K\), akkor a test mozgásegyenlete:
\(\displaystyle 2K-mg=\frac{mv^2}{R},\)
ahol \(\displaystyle R\) a parabola görbületi sugara a \(\displaystyle P\) pontban..
Az optikából ismert, hogy egy \(\displaystyle R\) sugarú gömbtükör fókusztávolsága közelítőleg \(\displaystyle R/2\). Ebből következik, hogy a parabolát legjobban közelítő kör (a simulókör) sugara
\(\displaystyle R=2f=\ell-d,\)
és így a keresett fonálerő:
\(\displaystyle K=\frac{1}{2}\left(mg+\frac{mg(\ell+d)}{\ell-d}\right)=mg\frac{\ell}{\ell-d}.\)
Statisztika:
65 dolgozat érkezett. 5 pontot kapott: Bukor Benedek, Elek Péter, Fekete Balázs Attila, Guba Zoltán, Jánosdeák Márk, Kolontári Péter, Kondákor Márk, Kozák András, Makovsky Mihály, Marozsák Tóbiás , Molnár Mátyás, Olosz Adél, Sal Dávid, Tófalusi Ádám, Vaszary Tamás, Viczián Anna. 4 pontot kapott: Bartók Imre, Beke Csongor, Berke Martin, Bíró Dániel, Csire Roland, Czett Mátyás, Édes Lili, Fajszi Bulcsú, Gulácsi Máté, Illés Gergely, Kozák 023 Áron, Mamuzsics Gergő Bence, Markó Gábor, Merkl Gergely, Morvai Orsolya, Pácsonyi Péter, Póta Balázs, Pszota Máté, Schneider Anna. 3 pontot kapott: 14 versenyző. 2 pontot kapott: 8 versenyző. 1 pontot kapott: 7 versenyző. 0 pontot kapott: 1 versenyző.
A KöMaL 2017. novemberi fizika feladatai