Problem P. 4974. (November 2017)

P. 4974. A thermally insulated cylinder is attached to a trolley. In the cylinder an easily moveable, and thermally insulated piston of mass $\displaystyle M=20$ kg separates two chambers of volume $\displaystyle V_0=50$ L, both containing air at a temperature of $\displaystyle T_0=300$ K, and at a pressure of $\displaystyle p_0=10^5$ Pa. The trolley moves towards a wall with speed $\displaystyle v = 10$ m/s, with which it collides totally inelastically. At most what may the temperature of the air be in that chamber which is closer to the wall?

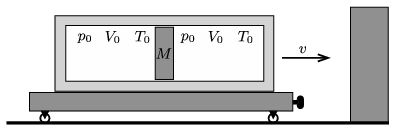
(5 pont)

Deadline expired on December 11, 2017.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. A rugalmatlan ütközés után a targonca és a tartály megáll, de a dugattyú $\displaystyle v$ kezdősebességgel tovább mozog. A tartályokban lévő levegő adiabatikusan összenyomódik, illetve kitágul, és emiatt felmelegszik, illetve lehűl.

Jelöljük a dugattyú legnagyobb elmozdulásához tartozó térfogatváltozást $\displaystyle kV_0$-lal, vagyis legyen a gázrészek térfogata ekkor $\displaystyle V_0(1+k)$, illetve $\displaystyle V_0(1-k)$. Mindkét gázrészre felírhatók az ideális gáz állapotegyenletei:

$\displaystyle \frac{pV}{T}=\text{állandó}, \qquad pV^{1{,}4} =\text{állandó}, \qquad E=\frac{5}{2}pV,$

ahol $\displaystyle E$ a gáz belső energiája. Kiszámíthatjuk, hogy a bal oldali gázrészre

$\displaystyle V_1=V_0(1+k ), \qquad p_1=p_0\left(\frac{V_0}{V_1}\right)^{1{,}4}=\frac{p_0}{\left(1+k\right)^{1{,}4}},\qquad T_1= \frac{T_0}{\left(1+k\right)^{0{,}4}}, \qquad E_1=\frac{5}{2}\frac{p_0V_0}{\left(1+k\right)^{0{,}4}},$

a jobb oldali részben levő levegőre pedig

$\displaystyle V_2=V_0(1-k ), \qquad p_2=p_0\left(\frac{V_0}{V_2}\right)^{1{,}4}=\frac{p_0}{\left(1-k\right)^{1{,}4}},\qquad T_2= \frac{T_0}{\left(1-k\right)^{0{,}4}}, \qquad E_2=\frac{5}{2}\frac{p_0V_0}{\left(1-k\right)^{0{,}4}}.$

A henger fala merev és hőszigetelő, tehát a benne lévő gázok és a dugattyú összenergiája nem változik:

$\displaystyle 2\cdot \frac{5}{2}p_0V_0+\frac{1}{2}Mv^2=E_1+E_2,$

vagyis

$\displaystyle \frac{1}{\left(1-k\right)^{0{,}4}}+\frac{1}{\left(1+k\right)^{0{,}4}}-2=\frac{Mv^2}{5p_0V_0}=0{,}08.$

Ennek az egyenletnek (pl. a http://www.wolframalpha.com/ program felhasználásával megkapható) megoldása $\displaystyle k\approx 0{,}38$, és a kérdezett hőmérséklet: $\displaystyle T_2=359~{\rm K}=86\,^\circ\rm C$.

Statistics:

47 students sent a solution.
5 points:	Andorfi István, Bartók Imre, Berke Martin, Bonifert Balázs, Csire Roland, Debreczeni Tibor, Édes Lili, Elek Péter, Fajszi Bulcsú, Fekete András Albert, Fekete Balázs Attila, Guba Zoltán, Illés Gergely, Kolontári Péter, Kondákor Márk, Kozák András, Makovsky Mihály, Markó Gábor, Marozsák Tóbiás , Máth Benedek, Olosz Adél, Ónodi Gergely, Pácsonyi Péter, Póta Balázs, Sal Dávid, Surján Botond, Tafferner Zoltán, Tófalusi Ádám, Turcsányi Ádám, Viczián Anna.
4 points:	Balaskó Dominik, Hajdu 046 Ákos, Mamuzsics Gergő Bence.
2 points:	12 students.
0 point:	2 students.

Problems in Physics of KöMaL, November 2017