A P. 4977. feladat (2017. november)

P. 4977. Az ábrán látható kapcsolásban a kapcsoló zárása előtt a kondenzátorok töltetlenek. Egy adott pillanatban zárjuk a kapcsolót. (Az áramforrás belső ellenállásától, a vezetékek és az ellenállások kapacitásától, továbbá a körben lévő elemek induktivitásától tekintsünk el.)

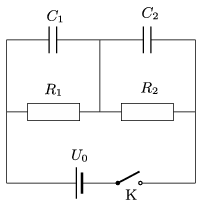
Ábrázoljuk vázlatosan a kondenzátorok feszültségét az idő függvényében!

Adatok: \(\displaystyle C_1=150~\mu\)F, \(\displaystyle C_2=50~\mu\)F, \(\displaystyle R_1=40~\rm k\Omega\), \(\displaystyle R_2=10~\rm k\Omega\), \(\displaystyle U_0=100\) V.

Nagy László (1931–1987) feladata

(5 pont)

A beküldési határidő 2017. december 11-én LEJÁRT.

Megoldás. Jelöljük a kondenzátorok feszültségét \(\displaystyle U_1(t)\) és \(\displaystyle U_2(t)=U_0-U_1(t)\) módon, az ellenállásokon folyó áramok pedig legyenek \(\displaystyle I_1\) és \(\displaystyle I_2\). (A feszültségeket és az áramokat jobbról balra tekintjük pozitívnak.)

A kapcsoló bekapcsolásának pillanatát követően a kondenzátorok nagyon rövid (elhanyagolható) idő alatt feltöltődnek, hiszen a vezetékek és a telep (belső) ellenállásasa elhanyagolható. Mivel a két kondenzátor közös pontjából csak az ellenállásokon keresztül folyhat el áram, a kezdeti pillanatban ott az össztöltés még nulla, vagyis a kondenzátorok feszültsége a kapacitásuk reciprokának arányában osztja meg a teljes telepfeszültséget.

\(\displaystyle U_1(0)=\frac{C_2}{C_1+C_2}U_0=25~{\rm V} \qquad \text{és}\qquad U_2(0)=\frac{C_1}{C_1+C_2}U_0=75~{\rm V}.\)

Elegendően hosszú idő múlva – amikor az ellenállásokon már állandó (és egymással megegyező) nagyságú áram folyik, az ellenállásokon azok nagyságával arányos feszültség alakul ki, és ugyanekkora lesz a hozzájuk kapcsolt kondenzátorok feszültsége is:

\(\displaystyle U_1^*=\frac{R_1}{R_1+R_2}U_0=80~{\rm V} \qquad \text{és}\qquad U_2^*=\frac{R_2}{R_1+R_2}U_0=20~{\rm V}.\)

A kondenzátorok feszültsége időben változó függvényekkel írható le, és vázlatosan az ábrán látható módon alakul. Belátható (de ez nem szerepelt a feladat kérdései között), hogy a feszültségváltozás az idő exponenciális függvénye, és az ábrán bejelölt 1,6 s a kapcsolás ,,időállandójának'' felel meg.

Megjegyzés. Belátjuk, hogy a feszültségek változása exponenciális függvénnyel adható meg, amelynek időállandóját mind a kondenzátorok, mind pedig az ellenállások párhuzamos kapcsolásának megfelelő képletből számíthatjuk ki:

\(\displaystyle T_0=R_\text{eredő}C_\text{eredő}=\frac{R_1R_2}{R_1+R_2}\,\left(C_1+C_2\right)=1{,}6~\rm s.\)

A folyamat során a kondenzátorok (időben változó) töltése: \(\displaystyle Q_1(t)=C_1U_1(t)\) és \(\displaystyle Q_2(t)=C_2\left(U_0-U_1(t)\right)\), tehát a rajtuk ,,átfolyó'' áram (a jobb oldali lemezekre ráfolyó és a bal oldali lemezekről elfolyó áram) erőssége:

\(\displaystyle I_1'=\frac{\Delta Q_1(t)}{\Delta t}=C_1\frac{\Delta U_1(t)}{\Delta t} \qquad \text{és}\qquad I_2'=\frac{\Delta Q_2(t)}{\Delta t}=-C_2\frac{\Delta U_1(t)}{\Delta t}. \)

Ugyanekkor az ellenállások árama:

\(\displaystyle I_1(t)=\frac{U_1(t)}{R_1} \qquad \text{és}\qquad I_2(t)=\frac{U_0-U_1(t)}{R_2}.\)

A csomóponti törvény szerint \(\displaystyle I_1+I_1'=I_2+I_2'\), vagyis

\(\displaystyle \left(C_1+C_2\right)\frac{\Delta U_1(t)}{\Delta t}+\left(\frac{1}{R_1}+\frac{1}{R_2} \right)U_1(t)=\frac{U_0 }{R_2}.\)

Az ellenállások és a kondenzátorok párhuzamos eredője

\(\displaystyle R_\text{eredő}=\left(\frac{1}{R_1}+\frac{1}{R_2} \right)^{-1}=8~\rm k\Omega,\qquad C_\text{eredő}=C_1+C_2=200~\mu\rm F.\)

Bevezetve a

\(\displaystyle \lambda=\frac{1}{R_\text{eredő}C_\text{eredő}}=\frac{1}{1{,}6~\rm s}\)

jelölést, a bal oldali kondenzátor feszültségváltozásának egyenlete:

\(\displaystyle \frac{\Delta U_1(t)}{\Delta t}=-\lambda U_1(t)+\text{állandó}.\)

Ennek az egyenletnek a kezdeti feltételt is figyelembe vevő megoldása (lásd. pl. a radioaktív bomlások hasonló egyenletét) SI egységekben:

\(\displaystyle U_1(t)=80-55\, e^{-\frac{t}{1{,}6}},\)

és hasonló módon

\(\displaystyle U_2(t)=20+55\, e^{-\frac{t}{1{,}6}}.\)

Statisztika:

20 dolgozat érkezett.
5 pontot kapott:	Bíró Dániel, Elek Péter, Fent István, Makovsky Mihály, Marozsák Tóbiás , Olosz Adél, Tófalusi Ádám, Turcsányi Ádám.
3 pontot kapott:	2 versenyző.
2 pontot kapott:	2 versenyző.
1 pontot kapott:	7 versenyző.
0 pontot kapott:	1 versenyző.

A KöMaL 2017. novemberi fizika feladatai