A P. 4990. feladat (2017. december)

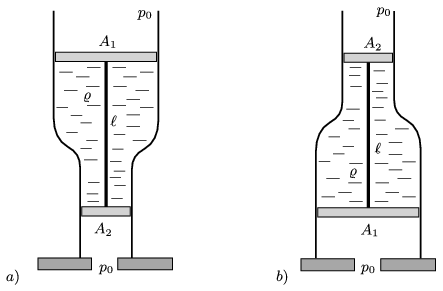
P. 4990. Egy függőleges tengelyű, rögzített cső szélesebb részének keresztmetszete $\displaystyle A_1$, a keskenyebb részé pedig $\displaystyle A_2$. A csőben két dugattyú és közöttük $\displaystyle \varrho$ sűrűségű folyadék van. A dugattyúkat $\displaystyle \ell$ hosszúságú, merev rúd köti össze. A dugattyúk és a rúd tömege elhanyagolható. A külső légnyomás $\displaystyle p_0$.

Mekkora és milyen irányú erő hat a rúdban, ha a cső

$\displaystyle a)$ a keskenyebb,

$\displaystyle b)$ a szélesebb

részére támaszkodik egy vízszintes lapon?

Milyen furcsaság történik akkor, ha $\displaystyle \ell$ ,,viszonylag nagy''?

A Kvant nyomán

(6 pont)

A beküldési határidő 2018. január 10-én LEJÁRT.

Megoldás. $\displaystyle a)$ Legyen a folyadék nyomása a felső dugattyúnál $\displaystyle p$, az alsónál pedig $\displaystyle p+\varrho g\ell$. Jelöljük a rúdban ébredő erőt $\displaystyle F$-fel, és akkor tekintsük pozitívnak, ha húzóerő alakul ki.

Az $\displaystyle a)$ esetben a dugattyúk mechanikai egyensúlyának feltétele:

$\displaystyle p_0A_1=pA_1-F,$

illetve

$\displaystyle p_0A_2=(p+\varrho g\ell)A_2-F.$

Ebből a két egyenletből következik, hogy

$\displaystyle F=\frac{A_1 A_2}{A_1-A_2}\varrho g \ell>0 \qquad \text{és}\qquad p=p_0+\frac{A_2}{A_1-A_2}\varrho g \ell>p_0.$

A folyadék nyomása tehát mindenhol nagyobb, mint a légköri nyomás, és a rúdban húzóerő ébred.

Hasonló módon számolhatunk a $\displaystyle b)$ esetben is ($\displaystyle A_1$ és $\displaystyle A_2$ szerepet cserélnek).

$\displaystyle F=-\frac{A_1 A_2}{A_1-A_2}\varrho g \ell<0 \qquad \text{és}\qquad p=p_0-\frac{A_1}{A_1-A_2}\varrho g \ell<p_0.$

A folyadék nyomása tehát ilyenkor a felső dugattyúnál kisebb, mint a légköri nyomás, és a rúdban nyomóerő ébred.

Érdekes helyzet áll elő, ha$\displaystyle \frac{A_1}{A_1-A_2}\varrho g\ell >p_0$. Ekkor a folyadék – a $\displaystyle b)$ esetben – elválik a felső dugattyútól (forrni kezd), majd a dugattyú és a rúd addig süllyed lefelé, amíg a felső dugattyú meg nem akad a szűkületnél.

Statisztika:

25 dolgozat érkezett.
6 pontot kapott:	Elek Péter, Fekete András Albert, Fekete Balázs Attila, Kondákor Márk, Marozsák Tóbiás , Máth Benedek, Olosz Adél, Sal Dávid.
5 pontot kapott:	Bartók Imre, Békési Ábel, Bonifert Balázs, Csire Roland, Makovsky Mihály, Póta Balázs, Sas 202 Mór, Schneider Anna, Tófalusi Ádám, Turcsányi Ádám.
4 pontot kapott:	1 versenyző.
3 pontot kapott:	1 versenyző.
1 pontot kapott:	5 versenyző.

A KöMaL 2017. decemberi fizika feladatai