A P. 5030. feladat (2018. április)

P. 5030. Egy \(\displaystyle 4d\) hosszúságú, \(\displaystyle m\) tömegű, szigetelő pálca végeihez ugyancsak \(\displaystyle m\) tömegű, kicsiny fémgömböket rögzítettünk. A pálca egyik végétől \(\displaystyle d\) távolságban egy \(\displaystyle m\) tömegű, átfúrt fémgömb található, amely súrlódásmentesen csúszhat a pálcán. Mindhárom fémgömbre \(\displaystyle Q\) töltést juttatunk, és a rendszert – egy űrállomáson lebegve – magára hagyjuk.

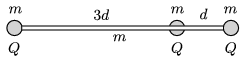
Mekkora lesz a középső gömb maximális sebessége, és mennyit mozdulnak el a testek a legnagyobb sebesség eléréséig?

Versenyfeladat nyomán

(4 pont)

A beküldési határidő 2018. május 10-én LEJÁRT.

Megoldás. Amikor a középső test sebessége maximális, a gyorsulása nulla, tehát a rá ható eredő erő is nulla. Ez a feltétel a szigetelő pálca közepénél, vagyis az egész rendszer tömegközéppontjában teljesül.

A tömegközéppont az átfúrt gömb kezdeti helyzetétől balra, attól

\(\displaystyle x=\frac{m\cdot 3d+m\cdot d-m\cdot d}{m+m+m+m}=\frac{3}{4}d\)

távolságra található. A tömegközéppont a mozgás során ugyanazon a helyen marad, tehát a legnagyobb sebesség eléréséig az átfúrt gömb \(\displaystyle (3/4)d\) távolságnyit mozdul el balra, a rúd pedig \(\displaystyle (1/4)d\) távolságnyit mozdul el jobbra.

Ha az \(\displaystyle m\) tömegű átfúrt fémgömb legnagyobb sebessége \(\displaystyle v\), akkor (a lendületmegmaradás törvénye szerint) a \(\displaystyle 3m\) össztömegű szigetelő pálca + a végeihez rögzített fémgömbökből álló rendszer sebessége \(\displaystyle v/3\). Az energiamegmaradás törvénye szerint:

\(\displaystyle \frac{1}{2}mv^2+\frac{1}{2}(3m)\left(\frac{v}{3}\right)^2=\frac{kQ^2}{d}\left(1+\frac13-\frac12-\frac12\right),\)

ahonnan az átfúrt gömb maximális sebessége (balra)

\(\displaystyle v=\sqrt{\frac{kQ^2}{2md}},\)

a szigetelő pálca legnagyobb sebessége pedig (jobbra)

\(\displaystyle 3v=3\sqrt{\frac{kQ^2}{2md}}.\)

Statisztika:

31 dolgozat érkezett.
4 pontot kapott:	Csuha Boglárka, Fajszi Bulcsú, Jánosik Áron, Makovsky Mihály, Marozsák Tóbiás , Máth Benedek, Olosz Adél, Sal Dávid, Tordai Tegze.
3 pontot kapott:	Bartók Imre, Illés Gergely, Kozák 023 Áron, Kozák András, Vaszary Tamás.
2 pontot kapott:	14 versenyző.
1 pontot kapott:	2 versenyző.
0 pontot kapott:	1 versenyző.

A KöMaL 2018. áprilisi fizika feladatai