 |
A P. 5047. feladat (2018. szeptember) |
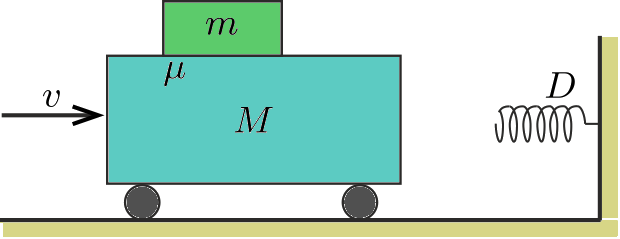
P. 5047. Az ábrán látható \(\displaystyle M\) tömegű kiskocsi és a rajta levő lapos, \(\displaystyle m\) tömegű hasáb \(\displaystyle v\) sebességgel halad a falhoz rögzített, \(\displaystyle D\) rugóállandójú nyomórugó felé. A hasáb és a kiskocsi felülete közötti súrlódási együttható \(\displaystyle \mu\).
a) Ütközéskor megcsúszik-e a hasáb?
b) Mennyi ideig tart az ütközés?
Adatok: \(\displaystyle M=0{,}2~\rm kg\), \(\displaystyle m=0{,}1~\rm kg\), \(\displaystyle v=1\) m/s, \(\displaystyle D=4{,}4~\)N/m, \(\displaystyle \mu=0{,}4\).
Közli: Németh László, Fonyód
(4 pont)
A beküldési határidő 2018. október 10-én LEJÁRT.
Megoldás. A rugóhoz nyomódó kiskocsi egy harmonikus rezgőmozgás fél periódusát teszi meg. A körfrekvencia:
\(\displaystyle \omega=\sqrt{\frac{D}{m+M}}=3{,}83~\rm s^{-1}.\)
Az \(\displaystyle A\) amplitúdójú rezgőmozgás kezdeti sebessége \(\displaystyle v=A\omega\), ahonnan
\(\displaystyle A=\frac{v}{\omega}=\frac{1}{3{,}83}\,{\rm m}\approx 26~\rm cm.\)
\(\displaystyle a)\) A kiskocsi és a rajta lévő hasáb maximális gyorsulása (ha a hasáb nem csúszik meg):
\(\displaystyle a_\text{max}=A\omega^2=v\omega=3{,}8~{\rm m/s}^2.\)
Ekkora gyorsulást a súrlódási erő akkor tud létrehozni, ha
\(\displaystyle a_\text{max}<\mu g\approx 3{,}9~{\rm m/s}^2.\)
Ez valóban fennáll, tehát a hasáb nem csúszik meg a kiskocsin.
\(\displaystyle b)\) Az ütközés ideje a teljes rezgésidő fele:
\(\displaystyle \Delta T=\frac{T}{2}=\frac{\pi}{\omega}=0{,}82~\rm s.\)
Statisztika:
98 dolgozat érkezett. 4 pontot kapott: Bekes Barnabás, Békési Ábel, Bokor Endre, Bonifert Balázs, Csépányi István, Debreczeni Tibor, Fekete András Albert, Fekete Levente, Fiam Regina, Fonyi Máté Sándor, Fülöp Sámuel Sihombing, Garamvölgyi István Attila, Gulácsi Máté, Györgyfalvai Fanni, Jánosdeák Márk, Kertész Balázs, Köpenczei Csenge, Laposa Hédi, Mácsai Dániel, Marozsák Tádé, Máth Benedek, Molnár Mátyás, Németh Kristóf, Olosz Adél, Rusvai Miklós, Sas 202 Mór, Schneider Anna, Stefán Boglárka Abigél, Sugár Soma, Sümegi Géza, Szoboszlai Szilveszter, Tafferner Zoltán, Takács Árpád, Tiefenbeck Flórián, Vaszary Tamás, Virág Levente. 3 pontot kapott: 23 versenyző. 2 pontot kapott: 10 versenyző. 1 pontot kapott: 25 versenyző. 0 pontot kapott: 2 versenyző. Nem számítjuk a versenybe a születési dátum vagy a szülői nyilatkozat hiánya miatt: 2 dolgozat.
A KöMaL 2018. szeptemberi fizika feladatai