 |
A P. 5065. feladat (2018. október) |
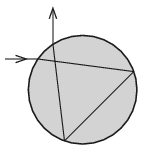
P. 5065. Egy gömb alakú vízcseppre érkező fénysugár az ábrán látható módon, két belső visszaverődés után a bejövő sugárra merőleges irányban lép ki a vízcseppből. Mekkora a beesési szög? (A víz törésmutatója \(\displaystyle n=\frac43\).)
Közli: Cserti József, Budapest
(5 pont)
A beküldési határidő 2018. november 12-én LEJÁRT.
Megoldás. A fénysugár eltérülése az egyenes iránytól összesen \(\displaystyle \tfrac{3}{2}\pi\) radián, vagyis \(\displaystyle 270^\circ\) (lásd az ábrát):

\(\displaystyle 2(\alpha-\beta)+2(180^\circ-2\beta)=270^\circ.\)
Innen \(\displaystyle \alpha=3\beta-45^\circ\) következik. Másrészt (a törési törvény értelmében) fennáll, hogy
\(\displaystyle \sin\alpha=\frac43\sin\beta,\)
vagyis
\(\displaystyle \sin(3\beta-45^\circ)=\frac43\sin\beta.\)
Ennek az egyenletnek – a feladat szempontjából elfogadható – numerikus megoldása \(\displaystyle \beta=27{,}8^\circ\), és ennek megfelelően a beesési szög: \(\displaystyle \alpha= 38{,}5^\circ\).
Statisztika:
38 dolgozat érkezett. 5 pontot kapott: Bokor Endre, Bukor Benedek, Conrád Márk, Csépányi István, Debreczeni Tibor, Elek Péter, Fülöp Sámuel Sihombing, Gál Péter Levente, Gulácsi Máté, Hartmann Alice, Hervay Bence, Jánosik Áron, Keltai Dóra, Mácsai Dániel, Makovsky Mihály, Markó Gábor, Marozsák Tádé, Merkl Levente, Molnár Mátyás, Morvai Orsolya, Olosz Adél, Rozgonyi Gergely, Rusvai Miklós, Sal Dávid, Tiefenbeck Flórián, Toronyi András, Tóth Ábel, Varga Vázsony. 4 pontot kapott: Jánosik Máté, Merkl Gergely, Murányi Albert, Osvárt Bence Attila, Solymosi Réka. 3 pontot kapott: 3 versenyző. 2 pontot kapott: 1 versenyző. 1 pontot kapott: 1 versenyző.
A KöMaL 2018. októberi fizika feladatai

