A P. 5067. feladat (2018. november)

P. 5067. Egy súrlódásmentes rúdra felfűzünk két könnyű rugót, amelyek rugóállandója \(\displaystyle D_1\), illetve \(\displaystyle D_2\). A rugók egyik vége rögzített, másik végeik közötti távolság \(\displaystyle d\). A rúdra felfűzött \(\displaystyle m\) tömegű, kis méretű testtel együtt az egyik rugót \(\displaystyle x\)-szel összenyomjuk, majd a testet elengedjük.

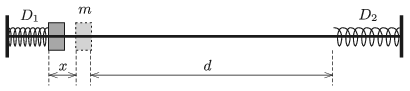
Mennyi idő múlva tér vissza elindulási helyére az \(\displaystyle m\) tömegű kis test? Függ-e ez az idő attól, hogy melyik rugóról indítjuk a testet?

Közli: Kobzos Ferenc, Dunaújváros

(4 pont)

A beküldési határidő 2018. december 10-én LEJÁRT.

Megoldás. Az összenyomott rugó rugalmas energiája megegyezik a ,,kilőtt'' test mozgási energiájával:

\(\displaystyle \frac{1}{2}D_1x^2=\frac{1}{2}mv^2,\)

vagyis a test sebessége \(\displaystyle v=x\sqrt{D_1/m}\) lesz. Ekkora sebességgel haladva

\(\displaystyle T_1=\frac{d}{v}=\frac{ d}{x }\sqrt{\frac{m}{D_1}}\)

idő alatt tesz meg \(\displaystyle d\) utat. Ehhez hozzáadódik még egy-egy negyedrezgés ideje a test megállásáig, a visszaérkezésig eltelt összes idő pedig

\(\displaystyle T=\pi\sqrt{m}\left(\frac{1}{\sqrt{D_1}}+\frac{1}{\sqrt{D_2}}\right)+\frac{2 d}{x }\sqrt{\frac{m}{D_1}}.\)

Ha a testet a másik rugótól indítjuk, a rezgések összes ideje változatlan marad, de az egyenletes mozgás ideje az erősebb rugónál kisebb lesz, tehát az összidő függ az indítás helyétől.

Statisztika:

88 dolgozat érkezett.
4 pontot kapott:	51 versenyző.
3 pontot kapott:	15 versenyző.
1 pontot kapott:	11 versenyző.
0 pontot kapott:	9 versenyző.
Nem versenyszerű:	2 dolgozat.

A KöMaL 2018. novemberi fizika feladatai