A P. 5069. feladat (2018. november)

P. 5069. Egy \(\displaystyle \alpha\) hajlásszögű lejtőre \(\displaystyle M\) tömegű, \(\displaystyle R\) sugarú, tömör hengert helyeztünk, amit egy vízszintes kötél köt össze a lejtő tetejével az ábrán látható módon. A test mellett található még egy \(\displaystyle m\) tömegű, \(\displaystyle r\) sugarú tömör henger. A két henger közötti súrlódás elhanyagolható, és az \(\displaystyle M\) tömegű henger nem emelkedik meg. Legalább mekkora az \(\displaystyle R\) sugarú henger és a lejtő közötti tapadási súrlódási együttható, ha a hengerek nem csúsznak meg a lejtőn?

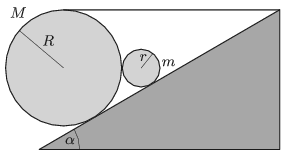
Adatok: \(\displaystyle \alpha=30^\circ\), \(\displaystyle R=3r\), \(\displaystyle M=3m\).

Közli: Takács Árpád, Budapest, Berzsenyi Dániel Gimnázium

(5 pont)

A beküldési határidő 2018. december 10-én LEJÁRT.

Megoldás. A megadott sugárarányok esetén a hengerek tengelyére illeszkedő sík

\(\displaystyle \varphi=\arcsin\frac{R-r}{R+r}=\arcsin\frac{1}{2}=30^\circ\)

nagyságú szöget zár be a lejtő síkjával, tehát a hengerek tengelye azonos magasságban helyezkedik el. A hengerekre az ábrán látható erők hatnak:

Itt már kihasználtuk, hogy a két henger között nincs súrlódás, tehát a közöttük fellépő erő vízszintes. Az \(\displaystyle M\) tömegű hengerre ható eredő forgatónyomaték nulla, emiatt a fonálban ébredő erő megegyezik az \(\displaystyle S\) súrlódási erővel. Az \(\displaystyle m\) tömegű hengerre sem hat forgatónyomaték, ami csak úgy lehetséges, ha a lejtő és ezen henger között nem lép fel súrlódási erő.

Az erők egyensúlyának feltétele:

\(\displaystyle F\,\frac{\sqrt{3}}{2}=mg,\)

\(\displaystyle \frac{1}{2}F=K,\)

\(\displaystyle Mg=\frac{1}{2}S+\frac{\sqrt{3}}{2}N,\)

\(\displaystyle K+\frac{1}{2}N=\left(1+ \frac{\sqrt{3}}{2} \right)S.\)

Ennek az egyenletrendszernek a megoldása:

\(\displaystyle F=\frac{2}{\sqrt{3}}mg,\)

\(\displaystyle K=\frac{1}{\sqrt{3}}mg,\)

\(\displaystyle S=\frac{(M+m)g}{2+\sqrt{3}},\)

\(\displaystyle N=(M+m)g-\frac{2}{\sqrt{3}}mg.\)

Az \(\displaystyle M\) tömegű henger akkor nem emelkedik fel a lejtőről, ha \(\displaystyle N\ge 0\), vagyis ha

\(\displaystyle M\ge \left(\frac{2}{\sqrt{3}}-1\right)m\approx 0{,}15\,m.\)

A megadott \(\displaystyle M=3m\) esetén ez teljesül. Az \(\displaystyle M\) tömegű henger akkor nem csúszik meg a lejtőn, ha (\(\displaystyle M=3m\) tömegarány mellett) a súrlódási együttható

\(\displaystyle \mu \ge \frac{S}{N} \approx 0{,}38.\)

Statisztika:

64 dolgozat érkezett.
5 pontot kapott:	Békési Ábel, Bokor Endre, Bukor Benedek, Csépányi István, Fekete Levente, Fiam Regina, Fülöp Sámuel Sihombing, Hartmann Alice, Havasi Márton, Horváth 127 Ádám, Jánosik Áron, Keltai Dóra, Laposa Hédi, Lipták Gergő, Mácsai Dániel, Marozsák Tádé, Máth Benedek, Merkl Gergely, Molnár Mátyás, Morvai Orsolya, Olosz Adél, Osztényi József, Pácsonyi Péter, Rusvai Miklós, Sal Dávid, Sas 202 Mór, Schneider Anna, Sugár Soma, Szoboszlai Szilveszter, Tafferner Zoltán, Telek Dániel, Tiefenbeck Flórián, Toronyi András, Turcsányi Máté, Varga Vázsony, Vaszary Tamás.
4 pontot kapott:	15 versenyző.
3 pontot kapott:	9 versenyző.
2 pontot kapott:	1 versenyző.
1 pontot kapott:	2 versenyző.
0 pontot kapott:	1 versenyző.

A KöMaL 2018. novemberi fizika feladatai