 |
A P. 5077. feladat (2018. november) |
P. 5077. Egy téglatest alakú, hőszigetelő falú tartály közepén jó hővezető anyagból készült dugattyú helyezkedik el. A dugattyútól balra \(\displaystyle V_0\) térfogatú levegő van, a dugattyútól jobbra \(\displaystyle V_0/2\) térfogatú, \(\displaystyle p_0=76~{\rm Hgcm}\approx 10^5\) Pa nyomású levegő és \(\displaystyle h=38\) cm magas higanyoszlop található. A tartály teljes szélessége (a dugattyú vastagságán felül) \(\displaystyle 2h\), magassága szintén \(\displaystyle 2h\).
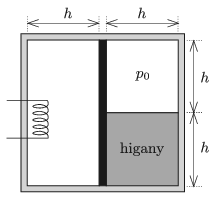
Egy beépített fűtőszállal lassan melegíteni kezdjük a bal oldali térrészt. A gázok hőmérséklete minden pillanatban megegyezik. Legfeljebb mekkora lehet a dugattyú elmozdulása, ha a higany, a tartály és a dugattyú hőtágulásától eltekintünk?
Közli: Berke Martin,
Zalaegerszegi Zrínyi Miklós Gimnázium
(6 pont)
A beküldési határidő 2018. december 10-én LEJÁRT.
Megoldás. Jelöljük a bal oldali részben lévő levegő kezdeti nyomását \(\displaystyle p_1\)-gyel (1. ábra), és számítsuk ki ennek nagyságát a dugattyú egyensúlyi feltételéből! Mivel (a megadott számadatok esetén) \(\displaystyle h\) magas higany hidrosztatikai nyomása éppen \(\displaystyle p_0/2\), a higany tetején a nyomás \(\displaystyle p_0\), a legalján pedig \(\displaystyle \tfrac 32 p_0\), így a higany átlagos nyomása \(\displaystyle \tfrac 54 p_0\). A dugattyú mélysége (az ábra síkjára merőleges irányú kiterjedése) \(\displaystyle \ell=V_0/(2h^2)\), de ez a mennyiség a továbbiakban érdektelen, minden képletből kiesik. A dugattyúra ható erők egyensúlyának feltétele:
| \(\displaystyle (1)\) | \(\displaystyle p_1\, 2h=p_0 \, h+\tfrac 54 p_0\cdot h,\qquad \text{azaz}\qquad p_1=\frac{9}{8}p_0.\) |
1. ábra
A két térfélben a levegő hőmérséklete ugyanakkora, hiszen a dugattyú anyaga jó hővezető. Ez a feltétel meghatározza a két gázmennyiség mólszámának arányát (ami a továbbiakban nyilván nem változik):
| \(\displaystyle (2)\) | \(\displaystyle \frac {n_\text{bal}}{n_\text{jobb}}=\frac{2h^2\cdot p_1}{ h^2\cdot p_0}=\frac{9}{4}.\) |
A fűtőszál bekapcsolása után a bal oldali térfélben is, és a jobb oldali részben is lassan felmelegszik a levegő (és vele együtt a higany is). Mindkét oldalon nő a levegő nyomása (ezek jelölése a 2. ábrán látható), és a dugattyú elmozdul valamekkora \(\displaystyle xh\) távolsággal. A higany (jó közelítéssel) összenyomhatatlan, emiatt a szintje valamekkora \(\displaystyle yh\) értékig megemelkedik, amint azt a 2. ábra mutatja. A higany átlagos nyomása (a teteje és az alja nyomásának számtani közepe): \(\displaystyle p_3+(y/4)p_0.\)
2. ábra
Tekintsünk most valamekkora \(\displaystyle x\) értékhez (elmozdulás-arányszámhoz) tartozó állapotot! A következő egyenleteket írhatjuk fel:
\(\displaystyle 2p_2h=p_3(2-y)h+(p_3+\frac{yp_0}{4})yh, \)
vagyis
| \(\displaystyle (3)\) | \(\displaystyle p_2=p_3+\frac{y^2}{8}p_0,\) |
továbbá a higany térfogatának állandósága miatt
| \(\displaystyle (4)\) | \(\displaystyle y(1-x)=1,\) |
és végül a gáztörvény szerint
| \(\displaystyle (5)\) | \(\displaystyle \frac{2p_2(1+x)}{p_3(2-y)(1-x)}=\frac {n_\text{bal}}{n_\text{jobb}}.\) |
Az (1)-(5) egyenletekből kifejezhetjük a két levegőrész nyomását, illetve a higanyszint magasságát \(\displaystyle x\) függvényében, és ezekből kiszámíthatjuk a rendszer energiájának megváltozását, ami a fűtőszál által leadott hővel egyenlő.
\(\displaystyle p_2=\frac{9(1-2x)}{8(1-x)^2(1-26x)}p_0,\)
\(\displaystyle p_3=\frac{1+x}{(1-x)^2(1-26x)}p_0.\)
Ha az \(\displaystyle x\) arányszám 0-tól indulva lassan növekszik, a két levegőrész nyomása fokozatosan emelkedik, és \(\displaystyle x\rightarrow \tfrac1{26}\) határesetben mindkettő végtelenhez tart, miközben a térfogatok és a higanyoszlop magassága véges nagyságú marad. Ez annyit jelent, hogy a rendszer energiájának akármilyen mértékű növelésével is legfeljebb \(\displaystyle x_{\rm max}h=\tfrac1{26}h\approx 15~\)mm-t mozdulhat el.
Megjegyzés. Reális körülmények között természetesen a határesetet megközelítő, vagy azt elérő elmozdulás ténylegesen nem következhet be, hiszen a korlátlanul növekvő nyomás és hőmérséklet hatására a tartály vagy szétrobban, vagy megolvad. Elég magas hőmérsékleten a higanygőz nyomása is számottevővé válik, a dugattyúra ható erők egyensúlyánál azt is figyelembe kell venni.
Statisztika:
23 dolgozat érkezett. 6 pontot kapott: Bokor Endre, Csépányi István, Elek Péter, Fülöp Sámuel Sihombing, Markó Gábor, Marozsák Tádé, Olosz Adél, Sal Dávid, Tiefenbeck Flórián. 5 pontot kapott: Vaszary Tamás. 4 pontot kapott: 1 versenyző. 3 pontot kapott: 4 versenyző. 2 pontot kapott: 5 versenyző. Nem versenyszerű: 3 dolgozat.
A KöMaL 2018. novemberi fizika feladatai