A P. 5081. feladat (2018. december)

P. 5081. Mekkora az ábrán látható ellenálláshálózat eredő ellenállása a \(\displaystyle C\) és \(\displaystyle D\) pontok között, ha mindegyik ellenállás \(\displaystyle R\) nagyságú? Hány százalékkal változik meg a \(\displaystyle C\) és \(\displaystyle D\) pontok közötti eredő ellenállás, ha az \(\displaystyle A\) és \(\displaystyle B\) pontok közötti ellenállást kivesszük?

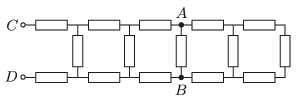
Közli: Tornyos Tivadar Eörs, Budapest

(4 pont)

A beküldési határidő 2019. január 10-én LEJÁRT.

Megoldás. Jobbról balra haladva egymás után kiszámíthatjuk az \(\displaystyle n\) ,,függőleges'' és hozzá kapcsolódó \(\displaystyle 2n\) ,,vízszintes'' ellenállás \(\displaystyle R_n\) eredőjét a vízszintes szárak két végpontja között (\(\displaystyle R\) egységekben):

\(\displaystyle R_1=3{,}000, \qquad R_{n+1}= \frac{R_n}{R_n+1}+2;\)

\(\displaystyle R_2 =\tfrac{11}{4}=2{,}750;\)

\(\displaystyle R_3=\tfrac{41}{15}=2{,}733;\)

\(\displaystyle R_4=\tfrac{153}{56}=2{,}732;\)

\(\displaystyle R_5=\tfrac{571}{209}=2{,}732=R_{CD}.\)

A ,,végtelen hosszú'' lánc ellenállása a

\(\displaystyle \frac{R_\infty}{R_\infty+1}+2=R_\infty\)

rekurziós formulából

\(\displaystyle R_\infty=1+\sqrt{3}=2{,}732.\)

Látható, hogy a létrakapcsolás eredő ellenállása nagyon gyorsan közelít a ,,végtelen hosszú'' létra eredőjéhez, már a háromfokú létrát jól közelíti az aszimptotikus képlet.

Hasonló módon kapjuk, hogy az \(\displaystyle A\) és \(\displaystyle B\) közötti ellenállás kiiktatása után:

\(\displaystyle R_1=3{,}000;\)

\(\displaystyle R_2 =\tfrac{11}{4}=2{,}750;\)

\(\displaystyle R_3=\tfrac{19}{4}=4{,}75;\)

\(\displaystyle R_4 =\tfrac{65}{23}=2{,}826;\)

\(\displaystyle R_5 =\tfrac{241}{88}=2{,}738=R_{CD};\)

(tehát kb. 0,24%-kal növekedett meg a \(\displaystyle C\) és \(\displaystyle D\) pontok közötti ellenállás)

\(\displaystyle \cdots\)

\(\displaystyle R_\infty=1+\sqrt{3}=2{,}732.\)

Itt az figyelhető meg, hogy a létra egyik ágának megváltoztatása ,,megzavarja'' ugyan a határértékhez közelítést, de a fokok számának növekedtével a sorozat hamar ,,elfelejti'' ezt a zavart, és néhány ,,lépés'' után már jól közelíti az aszimptotikus értéket.

Statisztika:

70 dolgozat érkezett.
4 pontot kapott:	Békési Ábel, Bokor Endre, Cseke Balázs, Endrész Balázs, Fekete Levente, Fiam Regina, Gál Péter Levente, Girus Kinga, Györgyfalvai Fanni, Hartmann Alice, Hervay Bence, Horváth 999 Anikó, Jánosik Áron, Jánosik Máté, Kalmár Dóra, Kárpáti Kristóf, Keltai Dóra, Kertész Balázs, Kovács Kristóf, Köpenczei Csenge, Lipták Gergő, Mácsai Dániel, Markó Gábor, Marozsák Tádé, Merkl Gergely, Merkl Levente, Molnár Mátyás, Murányi Albert, Nagy Balázs, Olosz Adél, Pácsonyi Péter, Pálfi Fanni, Rusvai Miklós, Sas 202 Mór, Schneider Anna, Selmi Bálint, Sugár Soma, Sümegi Géza, Tafferner Zoltán, Tanner Norman, Telek Dániel, Toronyi András, Tóth Ábel, Vajay Mónika, Vass Bence.
3 pontot kapott:	15 versenyző.
2 pontot kapott:	3 versenyző.
1 pontot kapott:	1 versenyző.
0 pontot kapott:	5 versenyző.
Nem számítjuk a versenybe a születési dátum vagy a szülői nyilatkozat hiánya miatt:	1 dolgozat.

A KöMaL 2018. decemberi fizika feladatai