 |
A P. 5089. feladat (2019. január) |
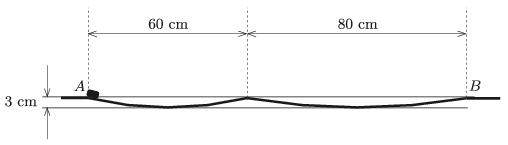
P. 5089. Az ábrán látható, súrlódásmentes pálya két körívből áll. A pálya \(\displaystyle A\) pontjából nagyon kicsi kezdősebességgel indulva csúszik egy apró test. Mennyi idő alatt jut el a test a görbült pálya jobb oldali végéig (a \(\displaystyle B\) pontig)?
Közli: Simon Péter, Pécs
(4 pont)
A beküldési határidő 2019. február 11-én LEJÁRT.
Megoldás. Egy \(\displaystyle d\) szélességű és \(\displaystyle h\) mélységű körív \(\displaystyle \ell\) sugara a Pitagorasz-tétel segítségével határozható meg:
\(\displaystyle \left(\frac{d}{2}\right)^2+(\ell-h)^2= \ell^2,\)
ahonnan
\(\displaystyle \ell= \frac{d^2}{8h}+\frac{h}{2}.\)
A feladat ábráján látható adatokkal a bal oldali körív sugara \(\displaystyle \ell_1=151{,}5\) cm, a jobb oldali körív sugara pedig \(\displaystyle \ell_2=268{,}2\) cm. A kicsiny test mozgása a köríveken éppen olyan, mint egy \(\displaystyle \ell_1\), illetve \(\displaystyle \ell_2\) hosszúságú fonálinga fél-fél lengése. (Ez jól látszik onnan, hogy – az energiamegmaradás törvénye szerint – mindkét mozgásnál a pályák egymásnak megfeleltethető pontjaiban ugyanakkora a test sebessége.) Az \(\displaystyle A\) pontból a \(\displaystyle B\) pontba jutás teljes időtartama tehát
\(\displaystyle T=\pi\sqrt{\frac{\ell_1}{g}}+\pi\sqrt{\frac{\ell_2}{g}}=\pi\left(\sqrt{\frac{1{,}51~\rm m}{9{,}81~\rm m/s^2}}+\sqrt{\frac{2{,}68~\rm m}{9{,}81\rm m/s^2}}\right)\,{\rm s}\approx2{,}9~{\rm s}.\)
Statisztika:
A KöMaL 2019. januári fizika feladatai