 |
A P. 5090. feladat (2019. január) |
P. 5090. Vízszintes talajon egy \(\displaystyle m\) tömegű, kocka alakú doboz áll. A doboz egyik lapjának közepéhez egy ugyancsak \(\displaystyle m\) tömegű, vékony, homogén pálca támaszkodik. Kezdetben mindkét testet rögzítetten tartjuk. A pálca és a talaj által bezárt szög \(\displaystyle \alpha=45^\circ\).
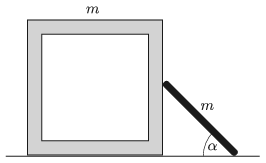
Mekkora gyorsulással indul el a doboz, ha a testeket elengedjük? (A súrlódás mindenhol elhanyagolható.)
Közli: Berke Martin, Zalaegerszeg, Zrínyi Miklós Gimnázium
(5 pont)
A beküldési határidő 2019. február 11-én LEJÁRT.
I. megoldás. Vegyük fel az egyes testekre ható erőket és a testek gyorsulását (szöggyorsulását) az 1. ábrán látható módon. Itt már kihasználtuk, hogy a tömegközépponti tétel értelmében a doboz és pálca tömegközéppontjának vízszintes gyorsulása egyenlő nagyságú, de ellentétes irányú.

1. ábra
A mozgásegyenletek:
| \(\displaystyle (1)\) | \(\displaystyle F=ma,\) |
| \(\displaystyle (2)\) | \(\displaystyle mg-N=mA,\) |
| \(\displaystyle (3)\) | \(\displaystyle N\frac{\ell}{2\sqrt2}-F\frac{\ell}{2\sqrt2}=\frac{m\ell^2}{12}\beta.\) |
Ezekhez a mozgásegyenletekhez két kényszerfeltétel (a pálca felső végének vízszintes irányú gyorsulására és az alsó végének függőleges irányú gyorsulására vonatkozó megszorítás) járul:
| \(\displaystyle (4)\) | \(\displaystyle a-\frac{\ell}{2}\beta \frac{1}{\sqrt2}=-a,\) |
| \(\displaystyle (5)\) | \(\displaystyle \frac{\ell}{2}\beta \frac{1}{\sqrt2}=A.\) |
Az (1)-(5) egyenletből az öt ismeretlen (\(\displaystyle F\), \(\displaystyle N\), \(\displaystyle a\), \(\displaystyle A\) és \(\displaystyle \beta\)) meghatározható, és a doboz keresett gyorsulására az
\(\displaystyle a=\frac{3}{13}g\)
eredmény adódik.
II. megoldás. Számítsuk ki az energiamegmaradás törvényének felhasználásával, hogy mekkora sebességre gyorsul fel a doboz az indítást követő nagyon rövid \(\displaystyle t\) idő alatt. Ha a testek sebessége (szögsebessége) a 2. ábrán látható nagyságú, akkor az energiatétel szerint
| \(\displaystyle (6)\) | \(\displaystyle \frac{1}{2}mv^2+\frac{1}{2}m\left(v^2+u^2\right)+\frac{1}{2}\, \frac{m\ell^2}{12}\omega^2=mgh,\) |
ahol \(\displaystyle h\) a pálca tömegközéppontjának lesüllyedése \(\displaystyle t\) idő alatt.

2. ábra
A kényszerfeltételek (miszerint a pálca végpontjai nem távolodnak el a doboztól, illetve a talajtól):
| \(\displaystyle (7)\) | \(\displaystyle \frac{\ell}{2}\omega \frac{1}{\sqrt2}-v=v,\) |
| \(\displaystyle (8)\) | \(\displaystyle \frac{\ell}{2}\omega \frac{1}{\sqrt2}-u=0.\) |
A (6)-(8) egyenletből (\(\displaystyle \beta\) kiküszöbölése után)
| \(\displaystyle (9)\) | \(\displaystyle \frac{26}{3}v^2=2gh\qquad \text{és} \qquad u=2v\) |
adódik.
Az indulást követő nagyon rövid idő alatt a doboz mozgása \(\displaystyle a\) gyorsulású egyenletesen változó mozgásnak tekinthető, és így a
\(\displaystyle v=at,\qquad \text{valamint} \qquad h=\frac{1}{2}ut=vt=at^2\)
összefüggések teljesülnek. Ezeket (9)-be helyettesítve a
\(\displaystyle \frac{26}{3}a^2t^2=2g\cdot at^2,\)
vagyis az
\(\displaystyle a=\frac{3}{13}g\)
végeredményt kapjuk.
Megjegyzés. Az energiamegmaradásra hivatkozó megoldás azért kényelmes, mert nincs szükség a belső erők (\(\displaystyle N\) és \(\displaystyle F\)) felvételére, hiszen ezek munkavégzése nulla.
Statisztika:
40 dolgozat érkezett. 5 pontot kapott: Bekes Barnabás, Csépányi István, Elek Péter, Hartmann Alice, Havasi Márton, Makovsky Mihály, Marozsák Tádé, Máth Benedek, Merkl Gergely, Olosz Adél, Sal Dávid, Szabó 314 László, Vass Bence. 4 pontot kapott: Bokor Endre, Sepsi Csombor Márton, Tiefenbeck Flórián. 3 pontot kapott: 5 versenyző. 2 pontot kapott: 1 versenyző. 1 pontot kapott: 18 versenyző.
A KöMaL 2019. januári fizika feladatai

