A P. 5092. feladat (2019. január)

P. 5092. Vízszintes helyzetű, jól hőszigetelt, rögzített hengert egy \(\displaystyle m\) tömegű, \(\displaystyle A\) keresztmetszetű, könnyen mozgó, rossz hővezető anyagból készült dugattyú két egyenlő, \(\displaystyle V_0\) térfogatú részre oszt. Az egyes részekben azonos mennyiségű, \(\displaystyle p_0\) nyomású héliumgáz van.

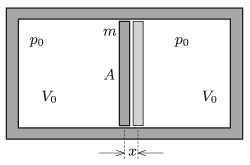
A dugattyút kissé kitérítjük egyensúlyi helyzetéből, majd magára hagyjuk. Mekkora lesz a rezgésidő?

Közli: Németh László, Fonyód

(5 pont)

A beküldési határidő 2019. február 11-én LEJÁRT.

Megoldás. Ha a dugattyút egy kicsiny \(\displaystyle x\) távolsággal elmozdítjuk – mondjuk – jobb felé, akkor a jobb oldali féltérben lévő gáz térfogata \(\displaystyle \Delta V=-xA\) értékkel megváltozik (lecsökken), a nyomása pedig

\(\displaystyle p_\text{jobb}=p_0+\Delta p\)

értékre növekszik. A héliumgáz belső energiája \(\displaystyle E=\frac32 pV\), a belső energia változása tehát

\(\displaystyle \Delta E=\frac32(p_0+\Delta p)(V_0-xA)-\frac32p_0V_0\approx \frac32p_0\Delta V+\frac32V_0\Delta p.\)

(A \(\displaystyle \Delta p\cdot \Delta V\)-vel arányos, ún. másodrendűen kicsiny tagot elhanyagoltuk.) A folyamat során a gáz

\(\displaystyle W'=p_0\Delta V=p_0Ax\)

tágulási munkát végez, miközben – a jó hószigetelés miatt – nem vesz fel hőt: \(\displaystyle Q=0\). A hőtan I. főtétele szerint

\(\displaystyle \Delta E+W'=Q=0,\)

vagyis

\(\displaystyle \frac{\Delta p}{p_0}+\frac{5}{3}\frac{\Delta V}{V_0}=0.\)

Megjegyzés. A fenti összefüggést úgy is megkaphatjuk, hogy a \(\displaystyle pV^{5/3}=\text{állandó}\) adiabatikus állapotegyenlet bal oldalának képezzük a kicsiny megváltozását, és azt nullával tesszük egyenlővé.

Látható, hogy a nyomás növekedése – közelítőleg – a dugattyú \(\displaystyle x\) elmozdulásával arányos, így a bal oldali térrészben a gáz nyomása ugyanilyen mértékben lecsökken,

\(\displaystyle p_\text{bal}=p_0-\Delta p\)

nagyságú lesz. A dugattyúra ható eredő erő a dugattyú \(\displaystyle x\) elmozdulása esetén:

\(\displaystyle F=\left(p_\text{bal}-p_\text{jobb}\right)A=-\frac{10}{3}\frac{A^2p_0}{V_0}\cdot x\equiv -Dx.\)

Ez az erőtörvény éppen olyan alakú, mint amilyen egy \(\displaystyle D\) rugóállandójú rugó esetében lenne. Ennek megfelelően az \(\displaystyle m\) tömegű dugattyú mozgása kis elmozdulások esetén harmonikus rezgőmozgás lesz, melynek rezgésideje

\(\displaystyle T=2\pi\sqrt{\frac{m}{D}}=2\pi\sqrt{\frac{3\,mV_0}{10\,p_0A^2}}.\)

Statisztika:

37 dolgozat érkezett.
5 pontot kapott:	Békési Ábel, Bokor Endre, Bonifert Balázs, Csépányi István, Elek Péter, Fiam Regina, Hartmann Alice, Klučka Vivien, Makovsky Mihály, Markó Gábor, Marozsák Tádé, Máth Benedek, Molnár Mátyás, Olosz Adél, Pácsonyi Péter, Sal Dávid, Szabó 314 László, Tiefenbeck Flórián, Vass Bence, Vaszary Tamás, Viczián Anna.
4 pontot kapott:	Hisham Mohammed Almalki, Pálfi Fanni.
3 pontot kapott:	7 versenyző.
2 pontot kapott:	5 versenyző.
1 pontot kapott:	2 versenyző.

A KöMaL 2019. januári fizika feladatai