A P. 5094. feladat (2019. január)

P. 5094. Három, $\displaystyle L=20~$cm hosszúságú szigetelőfonál egyik végéhez $\displaystyle m=1~$g tömegű, pontszerűnek tekinthető testeket erősítettek, amelyek töltése (egyenként) $\displaystyle Q=3{,}1\cdot 10^{-7}$ C. A fonalak másik végét közös pontban rögzítették. Kezdetben a feszes fonalak a függőlegessel $\displaystyle \alpha=30^\circ$-os szöget zárnak be, és a kis testek egy szabályos háromszöget alkotnak. Ezt követően egyszerre elengedjük a testeket.

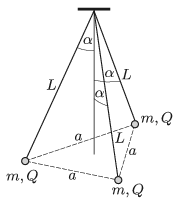
$\displaystyle a)$ Mekkora szöget zárnak be a fonalak a függőlegessel, amikor a testek sebessége maximális?

$\displaystyle b)$ Mekkora a testek legnagyobb sebessége?

Közli: Zsigri Ferenc, Budapest

(5 pont)

A beküldési határidő 2019. február 11-én LEJÁRT.

I. megoldás. $\displaystyle a)$ Amikor a testek sebessége maximális, akkor a sebességük nagysága nem változik, tehát a rájuk ható eredő erőnek nincsen a sebességükkel párhuzamos komponense.

Az elrendezés szimmetriája miatt a három test mindig szabályos háromszöget alkot, melynek oldalai

$\displaystyle \ell=\sqrt{3}L\sin\varphi$

hosszúságúak, ahol $\displaystyle \varphi$ a fonalaknak a függőlegessel bezárt szöge. (Kezdetben $\displaystyle \varphi=\alpha$ és $\displaystyle \ell=a$.)

Tekintsük az egyik testet, amely $\displaystyle L$ sugarú körpályán mozog. A testre függőlegesen lefelé $\displaystyle mg$ nehézségi erő, vízszintes irányban (a másik két test által kifejtett) $\displaystyle \sqrt{3}kQ^2/\ell^2$ nagyságú elektrosztatikus taszítóerő hat. Ezek eredője a legnagyobb sebességnek megfelelő helyzetben fonál irányú, vagyis

$\displaystyle mg\sin\varphi=\frac{kQ^2}{\sqrt{3}L^2\sin^2\varphi}\cos\varphi$

teljesül. Ezt az egyenletet

$\displaystyle \sin^3\varphi=\lambda\,\cos\varphi$

alakban is felírhatjuk, ahol

$\displaystyle \lambda=\frac{kQ^2}{\sqrt{3}mgL^2}=1{,}27.$

A fenti egyenlet $\displaystyle x=\tg\varphi$ helyettesítéssel harmadfokú egyenletté alakítható:

$\displaystyle x^2-1{,}27x^2-1{,}27=0,$

amelynek egyetlen valós gyöke $\displaystyle x=1{,}704$, azaz

$\displaystyle \varphi=59{,}6^\circ\approx 60^\circ.$

$\displaystyle b)$ A testek legnagyobb sebességét a rendszer összes (mozgási + gravitációs + elektrosztatikus) energiájának állandóságából határozhatjuk meg.

$\displaystyle -3mgL\cos\alpha+3\frac{kQ^2}{\sqrt{3}L\sin\alpha}=3\cdot\frac{1}{2}mv^2-3mgL\cos\varphi+3\frac{kQ^2}{\sqrt{3}L\sin\varphi},$

innen az ismert, illetve már kiszámított adatok behelyettesítése után kapjuk, hogy

$\displaystyle v=1{,}67~\frac{\rm m}{\rm s}.$

II. megoldás. Az energiamegmaradás tétele szerint (lásd az I. megoldást)

$\displaystyle \frac{v^2}{6gL}=\left(\cos\varphi- \frac{\sqrt{3}}{2}\right)+\lambda \left(2-\frac{1}{\sin\varphi}\right) \equiv f(\varphi).$

$\displaystyle a)$ A legnagyobb sebességű helyzetben az $\displaystyle f(\varphi)$ deriváltja eltűnik:

$\displaystyle -\sin\varphi+\lambda\frac{\cos\varphi}{\sin^2\varphi}=0,$

melynek numerikus megoldása (lásd pl. www.wolframalpha.com): $\displaystyle \varphi=\varphi_0=59{,}6^\circ.$

$\displaystyle b)$ A maximális sebesség: $\displaystyle v=\sqrt{2gL\cdot f(\varphi_0)}=1{,}67~\frac{\rm m}{\rm s}.$

Statisztika:

38 dolgozat érkezett.
5 pontot kapott:	Bekes Barnabás, Bokor Endre, Csépányi István, Lipták Gergő, Makovsky Mihály, Molnár Mátyás, Sal Dávid, Tiefenbeck Flórián, Vass Bence.
4 pontot kapott:	Hisham Mohammed Almalki, Jánosik Áron, Keltai Dóra, Marozsák Tádé, Máth Benedek, Merkl Gergely, Morvai Orsolya, Németh Csaba Tibor, Olosz Adél, Pácsonyi Péter, Toronyi András, Vaszary Tamás, Viczián Anna, Zámbori Zalán.
3 pontot kapott:	13 versenyző.
2 pontot kapott:	2 versenyző.

A KöMaL 2019. januári fizika feladatai