A P. 5102. feladat (2019. február)

P. 5102. Vízszintes talajon $\displaystyle m_1$ tömegű kiskocsi $\displaystyle v_0$ sebességgel halad az álló, $\displaystyle m_2$ tömegű kiskocsi felé. Mindkét kocsin egy-egy $\displaystyle m$ tömegű, lapos hasáb van. A hasábok és a kiskocsik felülete közötti tapadási súrlódási együttható $\displaystyle \mu_0$. Az álló kiskocsin $\displaystyle D$ rugóállandójú nyomórugó van.

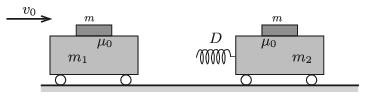
Ütközéskor megcsúszik-e valamelyik hasáb?

Adatok: $\displaystyle m_1=0{,}2~\rm kg$; $\displaystyle m_2=m=0{,}1~\rm kg$; $\displaystyle \mu_0=0{,}5$; $\displaystyle D=12~\rm N/m$; $\displaystyle v_0=1~\rm m/s$.

Közli: Németh László, Fonyód

(4 pont)

A beküldési határidő 2019. március 11-én LEJÁRT.

Megoldás. A kiskocsik ütközésekor a rugó egyre jobban összenyomódik, egyre nagyobb erőt fejt ki, és emiatt egyre nagyobb gyorsulást hoz létre a kiskocsikon. (A bal oldali kiskocsit lassítja, a jobb oldalit pedig gyorsítja.) A legnagyobb abszolút értékű gyorsulás a rugó legrövidebb állapotában jön létre, akkor, amikor a két kiskocsi egymáshoz viszonyított sebessége nulla, vagyis egyforma $\displaystyle u$ nagyságú sebességgel mozognak.

Tételezzük fel, hogy a lapos hasábok még ebben a helyzetben sem csúsznak meg a kiskocsikon. Ennek az a feltétele, hogy a kiskocsik gyorsulása ne haladja meg a $\displaystyle \mu_0 g$ értéket, hiszen a hasábok gyorsulását a tapadó súrlódási erő hozza létre, annak nagysága pedig legfeljebb $\displaystyle \mu mg$ lehet.

Jelöljük a kiskocsiknak a hasábbal megnövelt tömegét $\displaystyle M_1$-gyel és $\displaystyle M_2$-vel ($\displaystyle M_1=m_1+m=0{,}3~$kg, $\displaystyle M_2=m_2+m=0{,}2~$kg). A lendületmegmaradás törvénye szerint

$\displaystyle M_1v_0=\left(M_1+M_2\right)u,$

az energiamegmaradás törvénye pedig így alkalmazható):

$\displaystyle \frac{1}{2}M_1v_0^2=\frac{1}{2}\left(M_1+M_2\right)u^2+\frac{1}{2}Dx^2.$

Innen $\displaystyle u$ és $\displaystyle x$ kifejezhető az ismert adatokkal, nevezetesen

$\displaystyle x=v_0\sqrt{D\frac{M_1M_2}{M_1+M_2}}=0{,}1~\rm m,$

azaz a rugóerő maximális értéke

$\displaystyle F^\text{(max)}=Dx=1{,}2~\rm N.$

A kiskocsik maximális gyorsulása (ha létrejön ez az állapot)

$\displaystyle a_1^\text{(max)}=\frac{F^\text{(max)}}{M_1}=4~\frac{\rm m}{\rm s^2},\qquad a_2^\text{(max)}=\frac{F^\text{(max)}}{M_2}=6~\frac{\rm m}{\rm s^2}.$

Mivel $\displaystyle \mu_0 g\approx 5~ {\rm m}/{\rm s^2}$, látjuk, hogy a jobb oldali kiskocsin lévő lapos hasáb (még a rugó legnagyobb összenyomódása előtt) megcsúszik. Belátható, hogy a másik kiskocsin lévő hasáb sem ekkor, sem a későbbiekben nem csúszik meg, de a mozgás további részét nem a fenti egyenletek írják le.

Statisztika:

42 dolgozat érkezett.
4 pontot kapott:	Bekes Barnabás, Békési Ábel, Debreczeni Tibor, Erdélyi-Nagy Anna , Hervay Bence, Hubay Csenge, Kárpáti Kristóf, Köpenczei Csanád, Mácsai Dániel, Merkl Gergely, Morvai Orsolya, Olosz Adél, Rusvai Miklós, Sugár Soma, Szoboszlai Szilveszter, Tanner Norman, Toronyi András, Vass Bence, Virág Levente.
3 pontot kapott:	Fonyi Máté Sándor, Köpenczei Csenge, Ocskó Luca, Tafferner Zoltán, Vajay Mónika.
2 pontot kapott:	7 versenyző.
1 pontot kapott:	8 versenyző.
0 pontot kapott:	2 versenyző.
Nem számítjuk a versenybe a születési dátum vagy a szülői nyilatkozat hiánya miatt:	1 dolgozat.

A KöMaL 2019. februári fizika feladatai