A P. 5118. feladat (2019. március)

P. 5118. Egy $\displaystyle \alpha=30^\circ$-os hajlásszögű lejtőhöz két, egymástól $\displaystyle \ell=10$ cm távolságra lévő, egymással párhuzamos, elhanyagolható ellenállású sín van rögzítve, melyeket az egyik végüknél állandó $\displaystyle U_0$ feszültségű áramforrás kapcsol össze. A sínekre merőlegesen egy $\displaystyle M=30$ g tömegű, $\displaystyle R=0{,}2~\Omega$ ellenállású, vízszintes fémpálcát fektettünk, amely a síneken súrlódásmentesen mozoghat. A pálca közepéhez a sínekkel párhuzamos fonál csatlakozik, melynek elhanyagolható tömegű csigán átvetett függőleges darabjához egy $\displaystyle m=50~$g tömegű nehezék van erősítve. A berendezés függőlegesen lefelé mutató, $\displaystyle B=0{,}5$ T indukciójú, homogén mágneses mezőben van.

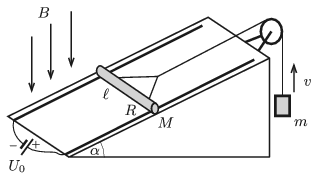
Mekkora legyen az áramforrás feszültsége, hogy az $\displaystyle m$ tömegű nehezék

$\displaystyle a)$ függőlegesen felfelé,

$\displaystyle b)$ függőlegesen lefelé $\displaystyle v=10~$m/s sebességgel egyenletesen haladjon?

Közli: Zsigri Ferenc, Budapest

(5 pont)

A beküldési határidő 2019. április 10-én LEJÁRT.

Megoldás. $\displaystyle a)$ A rúd a lejtőn lefelé mozog $\displaystyle v$ sebességgel, benne

$\displaystyle U_\text{ind}=B\ell v\cos\alpha$

feszültség indukálódik, ami a fémrúdban a külső áramforrással ellenkező irányban, tehát ,,balra'' irányuló,

$\displaystyle I=\frac{U_0-U_\text{ind}}{R}=\frac{U_0-B\ell v\cos\alpha}{R}$

nagyságú áramot hoz létre. Az áramjárta vezető rúdra a mágneses mező lejtőre merőleges $\displaystyle B\cos\alpha$ nagyságú komponense a lejtő esésvonalával párhuzamos, ,,lefelé'' irányuló, $\displaystyle F=BI\ell\cos\alpha$ nagyságú erőt fejt ki. A csigán átvetett fonalat $\displaystyle mg$ nagyságú erő feszíti (hiszen az $\displaystyle m$ tömegű test egyenletesen mozog), a rúd súlyának lejtő irányú komponense pedig $\displaystyle Mg\sin\alpha$.

Az egyenletesen mozgó rúd mozgásegyenlete:

$\displaystyle \frac{U_0-B\ell v\cos\alpha}{R}B\ell\cos\alpha+Mg\sin\alpha=mg,$

ahonnan a keresett feszültség:

$\displaystyle U_0=\frac{(m-M\sin\alpha)gR+vB^2\ell^2\cos^2\alpha}{B\ell\cos\alpha}=2{,}0~\rm V.$

$\displaystyle b)$ Ha az $\displaystyle m$ tömegű nehezék lefelé mozog állandó $\displaystyle v$ sebességgel, akkor a fenti végképletben $\displaystyle v$ helyett $\displaystyle -v$-t kell írnunk, és a szükséges feszültség:

$\displaystyle U_0=\frac{(m-M\sin\alpha)gR-vB^2\ell^2\cos^2\alpha}{B\ell\cos\alpha}=1{,}2~\rm V.$

Statisztika:

40 dolgozat érkezett.
5 pontot kapott:	Bokor Endre, Bukor Benedek, Czett Mátyás, Fiam Regina, Fülöp Sámuel Sihombing, Kalmár Dóra, Lipták Gergő, Máth Benedek, Molnár Mátyás, Morvai Orsolya, Sal Dávid, Telek Dániel, Tiefenbeck Flórián, Vass Bence.
4 pontot kapott:	Andorfi István, Békési Ábel, Bonifert Balázs, Debreczeni Tibor, Endrész Balázs, Hamar Dávid, Mácsai Dániel, Makovsky Mihály, Marozsák Tádé, Merkl Gergely, Olosz Adél, Szabó 314 László.
3 pontot kapott:	10 versenyző.
2 pontot kapott:	2 versenyző.
1 pontot kapott:	2 versenyző.

A KöMaL 2019. márciusi fizika feladatai