A P. 5144. feladat (2019. szeptember)

P. 5144. Egy \(\displaystyle \alpha\) hajlásszögű lejtő síkjára merőlegesen tartórudat rögzítünk. A rúd tetejéhez hozzáerősítjük egy \(\displaystyle \ell\) hosszúságú fonálinga felső végpontját. Az inga fonala \(\displaystyle \beta\) szöget zár be a lejtő síkjával.

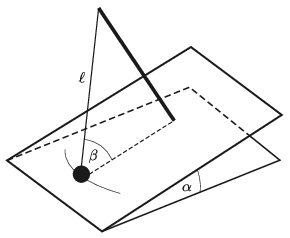
Mekkora az inga kis amplitúdójú lengéseinek periódusideje, ha \(\displaystyle \alpha+\beta < 90^\circ\), és a súrlódás elhanyagolható?

(4 pont)

A beküldési határidő 2019. október 10-én LEJÁRT.

Megoldás. Az inga nehezéke az inga síkjában egy olyan körön mozog, amelynek sugara \(\displaystyle r=\ell\cos\beta\). A mozgás – kis kitérések esetén – harmonikus rezgőmozgás, amelyet a nehézségi erő lejtő irányú komponense, vagyis \(\displaystyle g^*=g\sin\alpha\) hoz létre. A periódusidő tehát

\(\displaystyle T=2\pi\sqrt{\frac{r}{g^*}}= 2\pi\sqrt{\frac{\ell}{g }\,\frac{\cos\beta}{\sin\alpha}}.\)

Ez az idő a megadott egyenlőtlenség miatt biztosan nagyobb, mint az \(\displaystyle \ell\) hosszúságú fonálinga lengésideje. Ha az egyenlőtlenség nem teljesülne, az inga nehezéke nem maradna egyensúlyban az ábrán jelölt helyzetben.

Statisztika:

39 dolgozat érkezett.
4 pontot kapott:	Békési Ábel, Bonifert Balázs, Borbély András, Fiam Regina, Gurzó József, Hartmann Alice, Kertész Balázs, Kozaróczy Csaba, Ludányi Levente, Nguyễn Đức Anh Quân, Perényi Barnabás, Rusvai Miklós, Sepsi Csombor Márton, Somlán Gellért, Surányi Balázs, Toronyi András, Varga Vázsony, Viczián Anna.
3 pontot kapott:	Bohács Tamás, Fekete András Albert, Tanács Kristóf.
2 pontot kapott:	3 versenyző.
1 pontot kapott:	14 versenyző.
0 pontot kapott:	1 versenyző.

A KöMaL 2019. szeptemberi fizika feladatai