A P. 5160. feladat (2019. október)

P. 5160. Rögzített szigetelőállvány tetejére erősített kicsiny, $\displaystyle d=2$ cm átmérőjű fémgömb töltése $\displaystyle Q=8\cdot 10^{-9}$ C. Vékony, $\displaystyle \ell=1$ m hosszú, az ábra szerint felfüggesztett szigetelőszál végére erősített ugyanakkora semleges fémgömb tömege $\displaystyle m=1$ g. A fonalat $\displaystyle \alpha=60^\circ$-ig kitérítjük, majd elengedjük. A két gömb centrálisan, abszolút rugalmasan ütközik. Az ütközés során az elektromos mező energiája nem változik, energiadisszipáció nincsen.

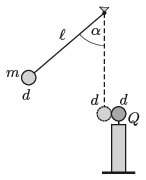
A kiindulási helyzeténél mennyivel kerül magasabbra a fonálinga kis gömbje, ha a légellenállás is elhanyagolható?

(Lásd még a kapacitásokról szóló cikket lapunk 425. oldalán.)

Közli: Holics László, Budapest

(5 pont)

A beküldési határidő 2019. november 11-én LEJÁRT.

Megoldás. Egy $\displaystyle R$ sugarú, önmagában álló fémgömb kapacitása $\displaystyle C=4\pi\varepsilon_0 R$. Ha ennek a gömbnek $\displaystyle Q$ töltése van, akkor az elektrosztatikus terének energiája

$\displaystyle W=\frac{Q^2}{2C}=\frac{Q^2}{8\pi\varepsilon_0R}.$

Ha olyan két töltött fémgömb esetét vizsgáljuk, amelyek az átmérőjükhöz viszonyítva elég távol vannak egymástól, akkor az egymáshoz viszonyított kapacitása (,,főkapacitása'') elhanyagolhatóan kicsi a szórt kapacitásukhoz képest, és ebben a közelítésben a rendszer elektrosztatikus energiája (lásd az idézett cikket!)

$\displaystyle W=\frac{Q_1^2}{8\pi\varepsilon_0R_1}+\frac{Q_2^2}{8\pi\varepsilon_0R_2},$

ahol $\displaystyle R_1=R_2=d/2$.

Esetünkben a kezdőállapotban $\displaystyle Q_1=0$ és $\displaystyle Q_2=Q$, az ütközés után pedig (a szimmetria és a töltésmegmaradás miatt) $\displaystyle Q_1=Q_2=\tfrac12Q$. Az ütközés után, amikor már ismét elég messze került a két gömb egymástól, a kapacitásuk megint elhanyagolhatóan kicsivé válik, és az energiájuk a szórt kapacitásukból számolható ki. (Közvetlenül az ütközés előtt és után az elektromos megosztás igen erős, emiatt az energia ezekben az állapotokban csak igen bonyolult módon számítható; erre azonban – szerencsére – nincs szükségünk.)

A rendszer elektrosztatikus energiájának megváltozása a fonálinga indítása és ismételt megállása között

$\displaystyle \Delta W=\frac{\left(\frac{1}{2}Q\right)^2}{4\pi\varepsilon_0 d}+\frac{\left(\frac{1}{2}Q\right)^2}{4\pi\varepsilon_0 d} - \frac{Q^2}{4\pi\varepsilon_0 d}=-\frac{Q^2}{8\pi\varepsilon_0 d}<0.$

A rendszer összes (elektrosztatikus+gravitációs helyzeti) energiája a folyamat során nem változik (a mozgási energia mind a kezdeti, mind pedig a végállapotban nulla), így a fonálinga kis gömbje a kiindulási helyzetéhez viszonyítva

$\displaystyle \Delta h=\frac{\vert\Delta W\vert}{mg}= \frac{Q^2}{8\pi\varepsilon_0mg d}=1{,}5~\rm mm$

távolsággal kerül magasabbra. (Az eredmény nem függ az inga $\displaystyle \ell$ hosszától.)

Megjegyzés. A megoldás során kihasználtuk, hogy a gömbök érintkezésekor, amikor a töltés fele átáramlik a másik gömbre, nincs energiaveszteség, mert a megosztás miatt a két gömb összeütközésekor már nullára csökkent közöttük a feszültség.

Más a helyzet akkor, amikor egy töltött és egy töltetlen síkkondenzátort kapcsolunk páruzamosan (lemezeiket páronként összeérintjük). Ekkor a kondenzátorok összenergiája lecsökken, az energiaváltozás a hirtelen kisüléskor keletkező szikrázás energiáját, a vezetékekben fejlődő Joule-hőt és elektromágneses sugárzás által elvitt energiát fedezi.

Ha a kondenzátorokat ,,kiméletesen'' érintjük össze, olymódon, hogy előbb a lemezeiket majdnem teljesen összetoljuk (de nem érintjük össze), annyira, hogy a feszültségük szinte nullára csökkenjen, majd a töltésátáramlás után ismét széthúzzuk a lemezeket az eredeti távolságukig. Az elektrosztatikus energia most is lecsökken, de az energiaváltozás éppen megegyezik a lemezek mozgatása közben végzett mechanikai munkával. Ez az eset felel meg a feladatban szereplő két fémgömb összeütközésének, de a gömbkondenzátorokhoz képest azzal az előnnyel rendelkezik, hogy egyszerű módon részletesen végigszámolható.

Statisztika:

17 dolgozat érkezett.
5 pontot kapott:	Bokor Endre, Varga Vázsony.
4 pontot kapott:	Takács Dóra, Viczián Anna.
3 pontot kapott:	12 versenyző.
2 pontot kapott:	1 versenyző.

A KöMaL 2019. októberi fizika feladatai