 |
A P. 5168. feladat (2019. november) |
P. 5168. Egy \(\displaystyle A\) alapterületű, \(\displaystyle m\) tömegű dugattyúval elzárt hengerben \(\displaystyle V_0\) térfogatú héliumgáz van. A dugattyút és a henger alját egy függőleges helyzetű, \(\displaystyle D=400\) N/m rugóállandójú, kezdetben nyújtatlan rugó köti össze.
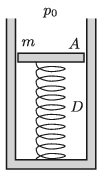
Mennyi hőt kell közölnünk a gázzal ahhoz, hogy a dugattyú \(\displaystyle h\) magassággal megemelkedjen, ha a rendszer hőszigetelt?
Adatok: \(\displaystyle A=7~\mathrm{dm}^2\), \(\displaystyle m=5\) kg, \(\displaystyle V_0=4~\mathrm{dm}^3\), \(\displaystyle D=400\) N/m, \(\displaystyle h=5\) cm és a külső légnyomás \(\displaystyle p_0=100\) kPa.
Közli: Kis Tamás, Heves
(4 pont)
A beküldési határidő 2019. december 10-én LEJÁRT.
Megoldás. Jelöljük a kezdőállapotot 1-es, a végállapotot 2-es indexszel. A gáz kezdeti térfogata
\(\displaystyle V_1=V_0=4~\rm dm^3,\)
a folyamat végén pedig
\(\displaystyle V_2=V_0+Ah=7{,}5~\rm dm^3.\)
Amikor a melegítés hatására a dugattyú \(\displaystyle x\) magassággal emelkedik, a gáz térfogata \(\displaystyle V=V_0+Ax\), a nyomása pedig (a dugattyúra ható erők egyensúlya miatt) \(\displaystyle p=p_0+\frac{mg+Dx}{A} \) lesz. Ebből a két összefüggésből \(\displaystyle x\) kiküszöbölése után kapjuk, hogy
\(\displaystyle p(V)=p_0+\frac{mg}{A}+\frac{V-V_0}{A^2}.\)
A nyomás a térfogat lineáris függvénye, tehát a folyamat a \(\displaystyle p_V\) diagramon egy egyenessel írható le. (Az ábra nem méretarányos!)
A kezdeti állapotban a nyomás
\(\displaystyle p_1=p_0+\frac{mg}{A}=100{,}7~\rm kPa,\)
a végállapotban pedig
\(\displaystyle p_2=p_0+\frac{mg+Dh}{A}=101{,}0~\rm kPa.\)
A folyamat során közölt hő a belső energia megváltozásának és a gáz által végzett munkának az összege. Az energiaváltozás:
\(\displaystyle E_2-E_1=\frac{3}{2}p_2V_2-\frac{3}{2}p_1V_1= 0{,}53~\rm kJ,\)
a gáz munkavégzése pedig
\(\displaystyle W'=\frac{p_1+p_2}{2}(V_2-V_1)=0{,}35~\rm kJ,\)
végül a közölt hő:
\(\displaystyle Q=\Delta E+W'=0{,}88~\rm kJ.\)
Megjegyzés. A gáz munkavégzése (a nyomások és a térfogatok behelyettesítése után) így is felírható:
\(\displaystyle W'=mgh+\frac{1}{2}Dh^2+p_0Ah.\)
Ebben a kifejezésben az egyes tagoknak szemléletes jelentése van. Az első a dugattyú gravitációs helyzeti energiájának növekedését adja meg. A második tag a rugóban tárolt rugalmas energiával egyenlő. Végül a harmadik tag azt a munkát adja meg, amennyi a \(\displaystyle p_0\) nyomású légkör \(\displaystyle Ah\) térfogatú részének ,,megemeléséhez'', a légkör helyzeti energiájának növeléséhez szükséges.
Statisztika:
53 dolgozat érkezett. 4 pontot kapott: Békési Ábel, Bonifert Balázs, Csécsi Marcell, Dékány Csaba, Fekete Levente, Fülöp Sámuel Sihombing, Hegymegi Balázs, Horváth 999 Anikó, Jánosik Áron, Kalmár Dóra, Kertész Balázs, Kozák Gergely, Kozaróczy Csaba, Németh Kristóf, Pálfi Fanni, Répási Tamás, Sepsi Csombor Márton, Somlán Gellért, Sümegi Géza, Szász Levente, Szoboszlai Szilveszter, Tanner Norman, Toronyi András, Török 111 László, Vass Bence, Viczián Anna. 3 pontot kapott: Bohács Tamás, Detki Pongrác, Fekete András Albert, Fiam Regina, Györgyfalvai Fanni, Hamar Dávid, Horváth Antal, Ludányi Levente, Nagyváradi Dániel, Rusvai Miklós, Sas 202 Mór, Schäffer Bálint, Selmi Bálint, Tanács Kristóf. 2 pontot kapott: 6 versenyző. 1 pontot kapott: 4 versenyző. 0 pontot kapott: 3 versenyző.
A KöMaL 2019. novemberi fizika feladatai