 |
A P. 5169. feladat (2019. november) |
P. 5169. Az \(\displaystyle L=20\) cm hosszúságú, homogén tömegeloszlású, \(\displaystyle m=0{,}4\) kg tömegű rudat az egyik végénél a bal oldali ábra szerint az \(\displaystyle A\) pontnál lévő csuklóhoz erősítjük, amely körül minden irányban foroghat. A rúd másik végét egy \(\displaystyle D=25\) N/m direkciós erejű, függőleges helyzetű, erőmentes állapotban szintén \(\displaystyle L\) hosszúságú rugóhoz rögzítjük. Kezdetben a rugó és a rúd egy egyenesbe esik. Ezt követően a rudat (a jobb oldali ábrán látható módon) \(\displaystyle \varphi=60^\circ\)-kal kitérítjük, majd elengedjük.
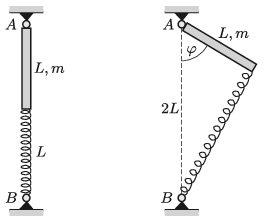
\(\displaystyle a)\) Mekkora sebességgel lendül át a rúd vége a függőleges helyzeten?
\(\displaystyle b)\) A rudat az egyensúlyi helyzetéből kis szöggel kitérítjük, majd elengedjük. Mennyi idő alatt jut a rúd függőleges helyzetbe?
\(\displaystyle c)\) Mekkora szögsebességgel kell a rugó-rúd rendszert a függőleges \(\displaystyle AB\) tengely körül forgatni, hogy a rúdnak a függőlegessel bezárt szöge folyamatosan \(\displaystyle 60^\circ\) legyen?
(A súrlódás mindenhol elhanyagolható.)
Közli: Zsigri Ferenc, Budapest
(5 pont)
A beküldési határidő 2019. december 10-én LEJÁRT.
Megoldás. \(\displaystyle a)\) A kitérített rúd, a megfeszített rugó és az \(\displaystyle AB\) szakasz derékszögű háromszöget alkot, a rugó hossza tehát \(\displaystyle \sqrt{3}\,L\), a megnyúlása pedig \(\displaystyle (\sqrt{3}-1)L\) lesz. A rúd tehetetlenségi nyomatéka az \(\displaystyle A\) pontra vonatkoztatva \(\displaystyle \tfrac13mL^2\), és a tömegközéppontja a függőleges helyzet eléréséig \(\displaystyle L/4\) távolsággal kerül mélyebbre. Alkalmazva a mechanikai energiamegmaradás tételét:
\(\displaystyle \frac{1}{2}D(\sqrt{3}-1)^2L^2+\frac{1}{4}mgL=\frac12\cdot \frac13 mL^2\omega^2,\)
ahonnan az adatok behelyettesítése után a rúd szögsebességére az \(\displaystyle \omega=13{,}2\, {\rm s}^{-1},\) a rúd végpontjának sebességére pedig a \(\displaystyle v=L\omega=2{,}64~\frac{\rm m}{\rm s}\) eredmény adódik.
\(\displaystyle b)\) A rudat kis szöggel kitérítve a rugó megnyúlása (és ezzel arányosan a rugóban ébredő erő) a kitérés négyzetével arányos, a rugóerőnek az \(\displaystyle A\) pontra vonatkozó forgatónyomatéka pedig közelítőleg a kitérés köbével arányos. Ez a forgatónyomaték a nehézségi erőnek a kitéréssel arányos forgatónyomatéka mellett elhanyagolhatóan kicsi, a rendszer tehát úgy mozog, mintha a rugó nem is volna ott. Ez annyit jelent, hogy a rúd mozgása olyan fizikai ingaként tárgyalható, amelynek lengésideje:
\(\displaystyle T=2\pi\frac{\frac13 mL^2}{\frac14 mgL}=\sqrt{\frac{2L}{3g}}=0{,}73~\rm s.\)
A kitérített, majd kezdősebesség nélkül elengedett rúd
\(\displaystyle \frac {T}4=0{,}18~\rm s\)
alatt kerül függőleges helyzetbe.
\(\displaystyle c)\) A rúd valamekkora \(\displaystyle \omega\) szögsebességgel forgó rendszerből nézve egyensúlyi helyzetben van, ezért az erők forgatónyomatékának előjeles összege nulla. A rúdra – ebben a forgó, nem inerciarendszerben – négyféle erő hat:
1. A \(\displaystyle G=mg=3{,}92~\)N nagyságú nehézségi erő, amelynek hatásvonala az \(\displaystyle A\) ponttól \(\displaystyle \tfrac12 L\,\sin 60^\circ=0{,}34~\rm m\) távol van.
2. A megfeszített rugóban fellépő erő nagysága \(\displaystyle F_1=D(\sqrt{3}-1)L=3{,}66~\rm N\), és a hatásvonala \(\displaystyle L=0{,}2~\rm m\) távol van az \(\displaystyle A\) ponttól.
3. A ,,centrifugális erő'', amelynek nagysága a tömegközéppontba képzelt \(\displaystyle m\) tömegű testre ható tehetetlenségi erő nagyságával egyezik meg: \(\displaystyle F_2=\tfrac12 mL\sin 60^\circ\,\omega^2=\omega^2\cdot 0{,}0346~\rm N\,s^2.\) Ennek az erőnek a hatásvonala azonban nem a tömegközépponton, hanem a rúd alsó harmadolópontján halad keresztül, tehát az \(\displaystyle A\) ponttól mért távolsága \(\displaystyle \tfrac23L\cos 60^\circ=0{,}0667~\rm m.\)
4. A rúdra hat még az \(\displaystyle A\) pontban (a csuklónál) egy ismeretlen nagyságú és ismeretlen irányú kényszererő, ennek azonban nincs forgatónyomatéka az \(\displaystyle A\) ponton átmenő tengelyre vonatkozóan.
Az erők forgatónyomatékának egyensúlyi feltétele:
\(\displaystyle F_1 L+G\frac{L}{2}\sin 60^\circ=\tfrac23L\cos 60^\circ F_2,\)
vagyis
\(\displaystyle 3{,}66\cdot 0{,}20+3{,}92\cdot 0{,}087= 0{,}0346~\rm s^2\cdot 0{,}0667 \cdot \omega^2.\)
Ebből a szögsebesség kiszámítható:
\(\displaystyle \omega=21{,}5~\frac{1}{\rm s}.\)
Statisztika:
27 dolgozat érkezett. 5 pontot kapott: Vass Bence. 4 pontot kapott: Fiam Regina, Fonyi Máté Sándor, Ludányi Levente, Szász Levente, Varga Vázsony. 3 pontot kapott: 7 versenyző. 2 pontot kapott: 6 versenyző. 1 pontot kapott: 7 versenyző. 0 pontot kapott: 1 versenyző.
A KöMaL 2019. novemberi fizika feladatai