 |
A P. 5173. feladat (2019. november) |
P. 5173. Egy N=2000 menetes, \displaystyle L=5 H induktivitású, elhanyagolható ohmos ellenállású körtekercs magja nagy mágneses permeabilitású gyűrű. A tekercs végeihez \displaystyle R=200~\Omega-os ellenállás csatlakozik. A tekercs egyik vége és ettől számított \displaystyle N_1=300-adik menete közé egy \displaystyle U_0=1{,}5 V feszültségű akkumulátor kapcsolható.
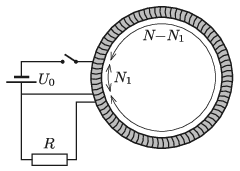
\displaystyle a) Mekkora áram folyik a tekercs két részén \displaystyle t_0=0{,}1 s-mal a kapcsoló zárása után?
\displaystyle b) Mekkora energiát ad le az áramforrás \displaystyle t_0 idő alatt, és mire fordítódik ez az energia?
A Kvant nyomán
(6 pont)
A beküldési határidő 2019. december 10-én LEJÁRT.
Megoldás. A kapcsoló zárása előtt a tekercs egyik részében sem folyik áram. A toroidtekercs magjában nulla a mágneses indukció, tehát mágneses fluxus sincs.
A kapcsoló zárását követően az \displaystyle N_1 menetes tekercsben \displaystyle I_1(t), a toroidtekercs többi részében \displaystyle I_2(t) áramerősség, a tekercs magjában pedig \displaystyle B(t) mágneses indukció alakul ki az 1. ábrán látható irányítással. A mágneses fluxus a tekercs magjában \displaystyle \Phi(t)=AB(t).

1. ábra
A gerjesztési törvény szerint (a tekercs magjában mindenhol) a mágneses indukció
| \displaystyle (1) | \displaystyle B(t)=\mu\frac{N_1I_1-(N-N_1)I_2}\ell |
nagyságú, a mágneses fluxus pedig
| \displaystyle (2) | \displaystyle \Phi(t)=B(t)\cdot A=\mu\frac{A}{\ell}\left[N_1\left(I_1+I_2\right)-NI_2\right]. |
Mivel az egész tekercs önindukciója
| \displaystyle (3) | \displaystyle L=\mu\frac{N^2A}{\ell} |
(\displaystyle \mu=\mu_0\,\mu_{\rm rel}\gg \mu_0), a mágneses fluxus így is felírható:
| \displaystyle (4) | \displaystyle \Phi(t)=\frac{L}{N^2}\left[N_1\left(I_1+I_2\right)-NI_2\right]. |
A Faraday-féle indukciótörvény szerint az időben változó mágneses fluxus a tekercsekben menetenként \displaystyle U=-\frac{\Delta \Phi}{\Delta t} feszültséget indukál. Kirchhoff huroktörvénye szerint a kapcsoló bekapcsolása után:
| \displaystyle (5) | \displaystyle U_0-N_1\frac{\Delta \Phi}{\Delta t}=0, |
| \displaystyle (6) | \displaystyle N\frac{\Delta \Phi}{\Delta t}-I_2R=0. |
Az (5) egyenlet meghatározza a mágneses fluxus időbeli változását:
\displaystyle \Phi(t)=\frac{U_0}{N_1}\cdot t=5~\frac{ \rm mH}{\rm s}\cdot t, \quad \text{ha}\quad t>0,
(6) pedig \displaystyle I_2-t:
\displaystyle I_2(t)=\frac{N}{N_1}\frac{U_0}{R}= \text{állandó}, \quad \text{ha}\quad t >0.
Ezt (4)-be helyettesítve megkapjuk \displaystyle I_1 időbeli változását, ha \displaystyle t>0:
\displaystyle I_1(t)=N\frac{N-N_1}{N_1^2}\,\frac{U_0}{R}+\frac{N^2}{N_1^2} \, \frac{U_0}{L}\,t=0{,}28~{\rm A}+13{,}3~\frac{\rm A}{\rm s}\cdot t.
A kérdéses \displaystyle t_0=0{,}1~s időpillanatban tehát a toroidtekercs két ágában
\displaystyle I_1(t_0)=1{,}61~{\rm A}\quad \text{és}\quad I_2(t_0)=50~{\rm mA}
erősségű áram folyik. A mágneses fluxus és az áramerősségek időbeli változását a 2. ábra mutatja.

2. ábra
Megjegyzés. A feladatban szereplő összeállítás egy transzformátor, amelynek primér körére – a szokásostól eltérő módon – egyenfeszültséget kapcsoltunk. A mágneses fluxus kezdetben az idővel arányosan növekszik, de egy idő után a tekercs magjának mágnesezettsége ,,telítésbe megy'', \displaystyle \mu_\text{rel} ekkor már nem tekinthető állandónak. A megoldás során feltételeztük, hogy \displaystyle t<t_0 időknél ez még nem következik be.
\displaystyle b) Kirchhoff csomóponti törvénye szerint az áramforráson átfolyó áram erőssége \displaystyle I_1(t)+I_2, amelynek átlagos értéke a \displaystyle 0<t<t_0 időintervallumban
\displaystyle I_\text{átlag}=\frac{I_1(0)+I_1(t_0)}{2}+I_2=1{,}00~\rm A,
az akkumulátor által \displaystyle t_0 idő alatt leadott energia tehát
\displaystyle W=I_\text{átlag}U_0\, t_0=0{,}15~\rm J.
Az ohmos ellenálláson fejlődő Joule-hő:
\displaystyle Q=I_2^2R\,t_0=0{,}05~\rm J.
Láthatóan \displaystyle W>Q, a különbségük feltehetően a kialakuló mágneses tér energiájával egyezik meg.
A mágneses mező energiasűrűsége
\displaystyle w_\text{mágn.}=\frac{B^2}{2\mu},
a tekercs \displaystyle A\ell térfogatú magjának energiája:
\displaystyle W_\text{mágn.}=A\ell w_\text{mágn.}=A\ell \frac{B^2}{2\mu}=\frac{\Phi^2(t_0)\ell}{2\mu A}=\frac{U_0^2}{2L} \left(\frac{N}{N_1}\right)^2 t_0^2=0{,}10~\rm J.
A ,,munkatétel'' teljesül:
\displaystyle W=Q+ W_\text{mágn.}.
Statisztika:
4 dolgozat érkezett. 6 pontot kapott: Bokor Endre. 1 pontot kapott: 1 versenyző. 0 pontot kapott: 2 versenyző.
A KöMaL 2019. novemberi fizika feladatai
|
|

