A P. 5188. feladat (2020. január)

P. 5188. Vízszintes felületen egyenes vonalban mozgó, téglatest alakú hasáb a súrlódás következtében egyenletesen lassul. Az ábra a hasáb mozgásának sebesség–idő grafikonját mutatja.

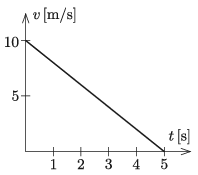
A hasáb tetejére rugós játékágyút rögzítettek, ami \(\displaystyle v_0\) torkolati sebességű, \(\displaystyle m\) tömegű lövedéket lő ki pillanatszerűen a hasáb lassuló mozgása során. A hasáb és az ágyú együttes tömege \(\displaystyle M\).

\(\displaystyle a)\) Milyen irányban álljon az ágyú csöve, hogy a kilövés egyáltalán ne legyen hatással a hasáb lassulására, vagyis a grafikon az ábra szerint folytatódjon a kilövés után is?

\(\displaystyle b)\) Ha az ágyúcsövet az előzőekben meghatározott szög felére engedjük le, akkor a kilövés milyen módon befolyásolja a lassulási grafikont? Ábrázoljuk a módosult sebesség-idő grafikont, ha a kilövés \(\displaystyle t=2\) s-nál következik be!

Adatok: \(\displaystyle m=0{,}1~\)kg, \(\displaystyle M=1~\)kg, \(\displaystyle v_0=5~\)m/s.

Közli: Honyek Gyula, Veresegyház

(5 pont)

A beküldési határidő 2020. február 10-én LEJÁRT.

Megoldás. A grafikonról leolvasható, hogy a hasáb gyorsulása: \(\displaystyle a=\mu g=-2~\frac{\rm m}{\rm s^2}\approx 0{,}2\,g\), tehát a csúszási súrlódási együttható közelítőleg 0,2. (A pontosabb érték: 0,204.) A hasábra a vízszintes felület olyan erőt fejt ki, amely a függőlegessel (a hasáb haladási irányához képest ,,hátrafelé'') \(\displaystyle \varphi=\arctg \mu=11{,}31^\circ\text{-os}\) szöget zár be.

A pillanatszerűnek tekintett (valójában csak nagyon rövid ideig tartó) kilövés során a lövedék hirtelen felgyorsul, tehát igen rövid \(\displaystyle \Delta t\) ideig nagyon nagy \(\displaystyle \boldsymbol F\) erő hat rá. A hasábra ugyancsak egy nagy erőlökés hat (amit a vízszintes felület fejt ki), ez akadályozza meg, hogy a hasáb függőleges irányban elmozduljon. A hasábra ható erőlökés iránya a függőlegessel ugyancsak \(\displaystyle \varphi\) szöget zár be, hiszen azt az \(\displaystyle \boldsymbol N\) nyomóerő és az \(\displaystyle \boldsymbol S\) súrlódási erő eredője hozza létre. A lendületmegmaradás törvénye szerint

\(\displaystyle a)\) Amennyiben a kilövés nincs hatással a hasáb mozgására (vagyis nem változik meg hirtelen a hasáb sebessége), akkor \(\displaystyle \Delta{ \boldsymbol v}_\text{hasáb}=0\), és így \(\displaystyle \boldsymbol F\) és \(\displaystyle \boldsymbol v_\text{lövedék}\) azonos irányú vektorok. Az előbbi a függőlegessel \(\displaystyle \varphi\) szöget zár be, a lövedék sebességét pedig az ágyúcső függőlegessel bezárt \(\displaystyle \gamma\) szöge határozza meg. Az (1) egyenlet csak akkor teljesülhet, ha \(\displaystyle \gamma=\varphi\), vagyis az ágyúcső a vízszintessel \(\displaystyle 90^\circ-\varphi=78{,}47^\circ\)-os szöget zár be.

Megjegyzés. A kilőtt lövedék sebességének benne kell lennie a hasáb sebessége és a függőleges által meghatározott síkban. Ha az ágyúcső ,,ferdén'' állna, akkor a lövedék ,,oldalirányú'' lendülete megváltoztatná a hasáb mozgásának irányát.

\(\displaystyle b)\) Változtassuk meg most az ágyúcsőnek a vízszintessel bezárt szögét az előző esetbeli szög felére, \(\displaystyle 39{,}23^\circ\)-ra, vagyis legyen az ágyúcső és a függőleges szöge \(\displaystyle \gamma'=50{,}77^\circ\).

A kilövés pillanatában (\(\displaystyle t=2~\rm s\)-nál az \(\displaystyle M+m\) tömegű rendszer \(\displaystyle v_1=6\) m/s sebességgel mozog, tehát a lendülete \(\displaystyle (M+m)v_1\). A kilövés hatására a hasáb sebessége hirtelen megváltozik, nagysága \(\displaystyle v_2\) lesz. Az \(\displaystyle m\) tömegű lövedék a hasábhoz képest \(\displaystyle v_0\cos\gamma'\) függőleges irányú és \(\displaystyle -v_0\sin\gamma'\) vízszintes irányú sebességre tesz szert. A lövedék vízszintes sebességkomponense a talajhoz képest \(\displaystyle v_2-v_0\sin\gamma'\) nagyságú. A függőleges irányú lendületváltozást az

\(\displaystyle N\Delta t=mv_y\)

erőlökés hozta létre. A vízszintes irányú erőlökés:

\(\displaystyle S\Delta t=-\mu N \Delta t= -\mu m v_y.\)

A vízszintes irányú lendületváltozást leíró egyenlet:

\(\displaystyle (Mv_2+m(v_2-v_0\sin\gamma')-(M+m)v_1= -\mu m v_0\cos\gamma',\)

ahonnan a hasáb sebességváltozása:

\(\displaystyle v_2-v_1=\frac{m}{M+m}v_0\cos\gamma'(\tg\gamma'-\mu).\)

(Látható, hogy ha \(\displaystyle \tg\gamma'=\mu\) teljesülne, akkor nem változna meg a hasáb sebessége a kilövés következtében, ahogy ezt már korábban beláttuk.) A leeresztett csövű ágyúnál viszont \(\displaystyle v_2-v_1=0{,}294~{\rm m/s}\approx 0{,}3~{\rm m/s}\), tehát a hasáb sebessége a kilövés hatására 6,3 m/s-ra nő. A hasáb a további mozgása során ugyanolyan ütemben lassul, mint korábban (hiszen a súrlódás miatti fékeződés üteme nem függ a mozgó test tömegétől).

Statisztika:

33 dolgozat érkezett.
4 pontot kapott:	Nguyễn Đức Anh Quân.
3 pontot kapott:	11 versenyző.
2 pontot kapott:	6 versenyző.
1 pontot kapott:	5 versenyző.
0 pontot kapott:	10 versenyző.

A KöMaL 2020. januári fizika feladatai