 |
A P. 5191. feladat (2020. január) |
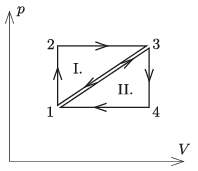
P. 5191. Ugyanannyi ideális gázzal az ábra szerinti p–V diagramon ábrázolt 1→2→3→1, illetve az 1→3→4→1 körfolyamatot végeztetjük. Melyik körfolyamatot végző gépnek nagyobb a hatásfoka, és milyen összefüggés áll fenn a két hatásfok között?
Varga István (1952–2007) feladata
(5 pont)
A beküldési határidő 2020. február 10-én LEJÁRT.
Megoldás. A gáz által végzett (hasznos) munka mindkét esetben ugyanannyi (W), ami a diagramon látható területekkel egyezik meg. Az I. körfolyamatban az 1→2 és a 2→3 állapotváltozások során vesz fel hőt a gáz, és a hatásfok
η1=WQ(1→2)+Q(2→3).
A II. körfolyamatban csak az 1→3 állapotváltozás során vesz fel hőt a gáz, így a hatásfok
η2=WQ(1→3).
Másrészt tudjuk, hogy
Q(1→2)+Q(2→3)+Q(3→1)=W,
hiszen egy teljes körfolyamat során a belső energia nem változik. Mivel Q(3→1)=−Q(1→3), teljesül, hogy
1η1−1η2=1,
vagyis η1<η2.
Annak ellenére, hogy külön-külön nem tudjuk kiszámítani a hatásfokokat, kifejezhetjük például a második körfolyamat hatásfokát az elsőével:
η2=η11−η1.
Statisztika:
27 dolgozat érkezett. 5 pontot kapott: Bokor Endre, Fekete András Albert, Fülöp Sámuel Sihombing, Hartmann Alice, Sas 202 Mór, Selmi Bálint, Somlán Gellért, Toronyi András, Vass Bence. 4 pontot kapott: Balázs 825 Ádám , Endrész Balázs, Fonyi Máté Sándor, Hamar Dávid, Horváth 999 Anikó, Kozák Gergely, Ludányi Levente, Rusvai Miklós, Szabados Noémi, Szász Levente, Viczián Anna. 3 pontot kapott: 3 versenyző. 2 pontot kapott: 2 versenyző. 1 pontot kapott: 1 versenyző. 0 pontot kapott: 1 versenyző.
A KöMaL 2020. januári fizika feladatai
|
|

