 |
A P. 5193. feladat (2020. január) |
P. 5193. Hat darab ohmos ellenállást az ábrán látható módon forrasztottunk össze. Mekkora eredő ellenállás mérhető a \(\displaystyle 20~\Omega\)-os ellenállás végpontjai között?
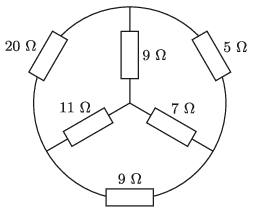
(Lásd A hídkapcsolás eredő ellenállása és áramerősségei című cikket a KöMaL 2016. évi 2. számában vagy a honlapon.)
Közli: Légrádi Imre, Sopron
(4 pont)
A beküldési határidő 2020. február 10-én LEJÁRT.
I. megoldás. Az áramkör alsó három, deltakapcsolású (más néven: háromszög kapcsolású) ellenállását az 1. ábrán látható csillagkapcsolással helyettesíthetjük. A megfelelő helyettesítő értékek (lásd pl. a ,,Négyjegyű'' megfelelő képleteit) ohm egységekben:
\(\displaystyle r_1=\frac{11}{3} \approx 3{,}67; \quad r_2=\frac{77}{27} \approx 2{,}85; \quad r_3=\frac{7}{3} \approx 2{,}33. \)
1. ábra
A sorosan kapcsolt ellenállások eredője \(\displaystyle 9+r_2=11{,}85,\) illetve \(\displaystyle 5+r_3=7{,}33\) ohm, majd ennek a két értéknek a párhuzamos eredője \(\displaystyle \left(\frac{1}{11{,}85}+ \frac{1}{7{,}33}\right)^{-1}=4{,}53\) ohm. Ezzel sorosan kapcsolva \(\displaystyle r_1\)-t az eredőjük 8,20 ohm, majd ezzel párhuzamosan kötve a 20 ohmos ellenállást megkapjuk a keresett eredőt:
\(\displaystyle R_\text{eredő}= \left(\frac{1}{8{,}20}+ \frac{1}{20}\right)^{-1}=5{,}8~\Omega.\)
Ugyanezt az eredmény úgy is megkaphatjuk, hogy az ábra közepén látható csillagkapcsolást alakítjuk át háromszög kapcsolássá.
II. megoldás. A kapcsolás a 20 ohmos ellenállást és vele párhuzamosan egy hídkapcsolást tartalmaz (2. ábra). A hídkapcsolás eredőjét a hivatkozott cikk képleteit alkalmazva kiszámíthatjuk, majd ezzel párhuzamosan kapcsoljuk a \(\displaystyle 20~\Omega\)-os ellenállást.
2. ábra
A végeredmény:
\(\displaystyle R_\text{eredő}=\frac{42\,460}{7303}~\Omega\approx 5{,}8~\Omega.\)
Megjegyzés. Az eredő ellenállás értékének valódi tört alakban történő megadása azt a téves képet sugallja, hogy az a tört az eredmény ,,pontos'' értéke, míg a tizedes törttel megadott alak csak közelítés. Ez csak akkor lenne igaz, ha az egész számokkal megadott ellenállásnagyságok (\(\displaystyle 20~\Omega\), \(\displaystyle 11~\Omega\), \(\displaystyle 5~\Omega\) stb.) ,,végtelen pontos'' adatok lennének; de biztosan nem azok! Indokoltabb tehát az eredmény tizedes tört alakban történő megadása, annyi kiírt számjeggyel, amennyit a bemenő adatok megadott számjegyei alapján jogosnak vélhetünk.
Statisztika:
37 dolgozat érkezett. 4 pontot kapott: Balogh Dávid, Endrész Balázs, Fekete András Albert, Fekete Levente, Fiam Regina, Fonyi Máté Sándor, Fülöp Sámuel Sihombing, Hamar Dávid, Jánosik Áron, Kertész Balázs, Kotán Tamás, Kovács Kristóf, Ludányi Levente, Németh Kristóf, Nguyễn Đức Anh Quân, Rusvai Miklós, Takács Dóra, Tóth Ábel, Varga Vázsony, Vass Bence. 3 pontot kapott: Balázs 825 Ádám , Bonifert Balázs, Horváth Antal, Jánosik Máté, Kozák Gergely, Páhán Anita Dalma, Perényi Barnabás, Schäffer Bálint, Sepsi Csombor Márton, Szász Levente, Török 111 László. 2 pontot kapott: 1 versenyző. 1 pontot kapott: 2 versenyző. 0 pontot kapott: 1 versenyző. Nem versenyszerű: 2 dolgozat.
A KöMaL 2020. januári fizika feladatai