 |
A P. 5203. feladat (2020. február) |
P. 5203. Egy \(\displaystyle 2A\) széles, átlátszó üveglemezben a lemez síkjára merőleges \(\displaystyle z\) tengely irányában változik a törésmutató, értéke \(\displaystyle z=\pm A\)-nál \(\displaystyle n_0\), míg \(\displaystyle z=0\)-nál \(\displaystyle n_1\). Az üveglemez szélénél (\(\displaystyle z=A\) ,,magasságban'') az \(\displaystyle x\) tengely irányában egy vékony lézersugarat indítunk, amely az üvegben eltérülve egy koszinuszgörbe mentén halad.
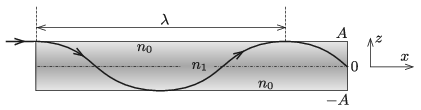
\(\displaystyle a)\) Hogyan függ a törésmutató \(\displaystyle z\)-től?
\(\displaystyle b)\) Mekkora a fény pályagörbéjének hullámhossza?
Adatok: \(\displaystyle A=1\) cm, \(\displaystyle n_0=1{,}5\) és \(\displaystyle n_1=1{,}6\).
(Lásd a P. 5066. feladat megoldását a KöMaL 2018. évi decemberi számában.)
Közli: Gnädig Péter, Vácduka
(5 pont)
A beküldési határidő 2020. március 10-én LEJÁRT.
I. megoldás. A fény pályájának egyenletét
| \(\displaystyle (1)\) | \(\displaystyle z(x)=A\cos(kx)\) |
alakban adhatjuk meg, ahol \(\displaystyle k=\frac{2\pi}{\lambda}\) (\(\displaystyle \lambda\) a koszinuszgörbe egyelőre még ismeretlen ,,hullámhossza'').
A Snellius–Descartes-törvény általánosított alakja szerint a rétegenként állandó, de a rétegekre merőleges irányban folytonosan változó törésmutató esetén is érvényes az
| \(\displaystyle (2)\) | \(\displaystyle n(z)\cdot \cos\varphi=K=\text{állandó}\) |
összefüggés, amelyben \(\displaystyle \varphi\) a görbe érintőjének az \(\displaystyle x\) tengellyel bezárt szöge. Ennek a szögnek a tangense a görbe – helyről helyre változó – meredekségével, vagyis az \(\displaystyle n(z)\) függvény deriváltjával egyezik meg. Ez a meredekség (a deriválás szabályaiból, vagy egy analógia, a harmonikus rezgőmozgás ismert út- és sebességfüggvényének vizsgálatából adódóan)
\(\displaystyle \tg\varphi=-Ak\sin(kx), \)
ami (1) szerint így is írható:
| \(\displaystyle (3)\) | \(\displaystyle \tg\varphi=-k\sqrt{A^2-z^2}.\) |
Mivel
| \(\displaystyle (4)\) | \(\displaystyle \cos\varphi=\frac{1}{\sqrt{1+\tg^2\varphi}},\) |
a törési törvény (2) összefüggése (3) és (4) felhasználásával így alakul:
\(\displaystyle n(z)=K\sqrt{1+k^2(A^2-z^2)}.\)
Mivel \(\displaystyle n(x=A)=n_0\) és \(\displaystyle n(x=0)=n_1\), a \(\displaystyle K\) és \(\displaystyle k\) állandókat meghatározhatjuk:
\(\displaystyle K=n_0 \qquad \text{és}\qquad k=\frac{1}{A}\sqrt{\left(\frac{n_1}{n_0}\right)^2-1}.\)
A törésmutató keresett alakja tehát
\(\displaystyle n(z)=\sqrt{n_1^2-(n_1^2-n_0^2)\frac{z^2}{A^2}}=\sqrt{2{,}56-0{,}31\frac{z^2}{(1\,\rm cm)^2}},\)
és a fény pályagörbéjének hullámhossza:
\(\displaystyle \lambda=2\pi\frac{n_0A}{\sqrt{n_1^2-n_0^2}}\approx 17~\rm cm.\)
II. megoldás. A Maupertuis-elv (legkisebb hatás elve) szerint (lásd a P. 5066. feladat megoldását és a Variációs elvek a klasszikus és a kvantumfizikában c. cikket a KöMaL 2018. évi decemberi számában) a helyről helyre változó törésmutató és a fénypálya alakja között ugyanolyan összefüggés van, mint valamilyen erő hatására mozgó tömegpont helyről helyre változó sebességnagysága és a részecske pályagörbéje között.
A feladatban szereplő koszinuszgörbe alakú mozgás a klasszikus mechanikában úgy valósul meg, ha egy test \(\displaystyle z\) tengely irányában harmonikus rezgőmozgást végez, miközben az \(\displaystyle x\) tengely irányában egyenletesen halad:
| \(\displaystyle (5)\) | \(\displaystyle z(t)=A\cos(\omega t) \qquad\text{és}\qquad x=v_0t.\) |
Az időt kiküszöbölve a pályagörbe egyenletéhez jutunk:
| \(\displaystyle (6)\) | \(\displaystyle z(x)=A\cos\frac{\omega}{v_0}x.\) |
Ilyen mozgást egy olyan \(\displaystyle D=m\omega^2\) rugóállandójú rugó képes létrehozni, ami a \(\displaystyle z\) tengely irányában a kitéréssel arányos erőt fejt ki, de az \(\displaystyle x\) tengely mentén szabad mozgást enged meg. Ebben az esetben az energiamegmaradás törvénye így írható fel:
\(\displaystyle \frac12Dz^2+\frac12mv^2=E =\text{állandó},\)
vagyis
| \(\displaystyle (7)\) | \(\displaystyle v(z)= \sqrt{\frac{2E}{m} -\frac{D}{m}z^2}.\) |
(Itt \(\displaystyle v=\vert \boldsymbol v\vert\) a test teljes sebességének nagyságát jelöli.) Mivel \(\displaystyle z=A\) esetben \(\displaystyle v=v_0\), a teljes energia
\(\displaystyle E=\frac12 mv_0^2+\frac12 DA^2,\)
és a test sebességének képlete:
| \(\displaystyle (8)\) | \(\displaystyle v(z)=\sqrt{v_0^2+\left(A^2-z^2\right)\omega^2}.\) |
Az optikai Fermat-elv és a mechanikai Maupertuis-elv közötti hasonlóság alapján mondhatjuk, hogy a koszinusz alakú fénygörbe akkor valósulhat meg, ha a törésmutató a \(\displaystyle z\) koordinátának ugyanolyan függvénye, mint \(\displaystyle v(z)\), attól legfeljebb egy arányossági tényezőben térhet el. (Az arányossági tényező a Fermat-féle minimumelvben nyilván nem játszik szerepet.) Érvényes tehát, hogy
| \(\displaystyle (9)\) | \(\displaystyle n(z)=\alpha\sqrt{v_0^2+\left(A^2-z^2\right)\omega^2},\) |
ahol \(\displaystyle \alpha\) egy tetszőlegesen választható állandó.
Felhasználva a megadott \(\displaystyle n(\pm A)=n_0\) és \(\displaystyle n(0)=n_1\) értékeket, megkapjuk, hogy
\(\displaystyle n_0=\alpha v_0 \qquad \text{és} \qquad n_1=\alpha\sqrt{v_0^2+A^2\omega^2},\)
vagyis
\(\displaystyle v_0=\frac{n_0}{\alpha}, \qquad \text{továbbá} \qquad \omega= \frac{\sqrt{n_1^2-n_0^2}}{\alpha A}.\)
Ezeket visszahelyettesítve (9)-be kapjuk, hogy
\(\displaystyle n(z)=\sqrt{n_1^2-(n_1^2-n_0^2)\frac{z^2}{A^2}},\)
és a fénypálya hullámhossza (6) szerint:
\(\displaystyle \lambda=2\pi \frac{v_0}{\omega}= 2\pi\frac{n_0A}{\sqrt{n_1^2-n_0^2}}.\)
Statisztika:
7 dolgozat érkezett. 5 pontot kapott: Bokor Endre, Ludányi Levente, Selmi Bálint, Tóth Ábel, Varga Vázsony. 4 pontot kapott: Horváth 999 Anikó. 3 pontot kapott: 1 versenyző.
A KöMaL 2020. februári fizika feladatai

