A P. 5209. feladat (2020. március)

P. 5209. Az ábrán látható csigasorban a legfelső állócsiga 15 cm, a legalsó mozgócsiga pedig 25 cm sugarú. A mozgócsigák mindegyike 15-öt fordul percenként, és az állócsigák fordulatszáma is megegyezik egymással. (A csigák közötti kötéldarabok függőlegesnek tekinthetők.)

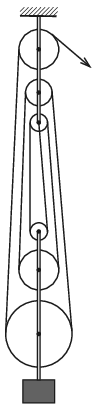
\(\displaystyle a)\) Mekkora a többi csiga sugara?

\(\displaystyle b)\) Mekkora az állócsigák fordulatszáma?

Közli: Baranyai Klára, Veresegyház

(4 pont)

A beküldési határidő 2020. április 14-én LEJÁRT.

Megoldás. Jelölje a csigák sugarát fentről lefelé haladva \(\displaystyle r_1,\) \(\displaystyle r_2,\) \(\displaystyle r_3,\) \(\displaystyle r_4,\) \(\displaystyle r_5\) és \(\displaystyle r_6\). Tudjuk, hogy \(\displaystyle r_1=15~\)cm és \(\displaystyle r_6=25~\)cm. Legyen továbbá az állócsigák fordulatszáma \(\displaystyle f\), a mozgócsigáké pedig \(\displaystyle f'=15~\text{perc}^{-1}\).

Ha a mozgócsigák egymással összekapcsolt tengelye \(\displaystyle v\) sebességgel emelkedik, akkor az egyes kötéldarabok sebessége az ábrán jelölt értékű. A csigák kerületi pontjainak sebessége a csiga tengelyéhez viszonyítva fentről lefelé haladva \(\displaystyle 6v\), \(\displaystyle 4v\), \(\displaystyle 2v\), \(\displaystyle v\), \(\displaystyle 3v\), \(\displaystyle 5v\). Ezek a kerületi sebességek kifejezhetők a csigák fordulatszáma és sugara segítségével:

\(\displaystyle 6v=2\pi r_1f,\qquad 4v=2\pi r_2f,\qquad 2v=2\pi r_3f,\)

vagyis

\(\displaystyle r_1:r_2:r_3=3:2:1, \qquad \text{ahonnan}\qquad r_2=10~{\rm cm}\quad \text{és}\quad r_3=5~\rm cm.\)

Hasonló módon a mozgócsigákra felítható, hogy

\(\displaystyle v=2\pi r_4f',\qquad 3v=2\pi r_5f',\qquad 5v=2\pi r_6f',\)

vagyis

\(\displaystyle r_4:r_5:r_6=1:3:5, \qquad \text{ahonnan}\qquad r_4= 5~{\rm cm}\quad \text{és}\quad r_5=15~\rm cm.\)

Az állócsigák fordulatszáma:

\(\displaystyle f=\frac{2r_4}{r_3}f'=30~\text{perc}^{-1}.\)

Megjegyzés. Jóllehet nem volt kérdés, de azt is kiszámíthatjuk még, hogy a teher

\(\displaystyle v=150\pi ~\frac{\rm cm}{\rm perc}=0{,}079~\frac{\rm m}{\rm s}\)

sebességgel emelkedik. A kötél végét \(\displaystyle 6v\) sebességgel kell mozgatnunk, de csak a teher súlya hatodrészének megfelelő erőt kell kifejtenünk.

Statisztika:

12 dolgozat érkezett.
4 pontot kapott:	Hamar Dávid, Jánosik Máté, Ludányi Levente, Páhán Anita Dalma, Somlán Gellért.
3 pontot kapott:	Sepsi Csombor Márton.
1 pontot kapott:	1 versenyző.
0 pontot kapott:	4 versenyző.
Nem számítjuk a versenybe a születési dátum vagy a szülői nyilatkozat hiánya miatt:	1 dolgozat.

A KöMaL 2020. márciusi fizika feladatai