A P. 5211. feladat (2020. március)

P. 5211. Mekkora kezdősebességgel kell meglökni a $\displaystyle 2L$ hosszúságú, vízszintes pálya elején álló kis testet, hogy a vízszintes pálya végén lévő $\displaystyle R$ sugarú, függőleges félkör alakú pályán végigcsúszva a vízszintes szakasz felezőpontjába csapódjon be?

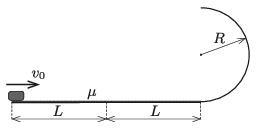
A vízszintes pályán a súrlódási együttható $\displaystyle \mu$, a félkör alakú pálya súrlódásmentes.

Adatok: $\displaystyle L=2$ m; $\displaystyle R=0{,}5$ m; $\displaystyle \mu=0{,}4$.

Közli: Kobzos Ferenc, Dunaújváros

(4 pont)

A beküldési határidő 2020. április 14-én LEJÁRT.

Megoldás. Jelöljük a kis test sebességét a félkör legfelső pontjánál $\displaystyle v_1$-gyel! Mivel a félkört elhagyva a test vízszintes hajítást végez, és $\displaystyle 2R$ magasságból indulva $\displaystyle t$ idő alatt $\displaystyle L$ utat tesz meg vízszintes irányban, felírható, hogy

$\displaystyle 2R=\frac{g}{2}\,t^2,\qquad L=v_1t,$

ahonnan

$\displaystyle v_1^2=\frac{L^2g}{4R}.$

Megjegyzés. Ez a sebesség a kényszerpálya elhagyása előtti pillanatban

$\displaystyle a=\frac{v_1^2}{R}=\left(\frac{L}{2R}\right)^2 g=4g$

centripetális gyorsulásnak felel meg. Mivel $\displaystyle a>g$, a test sem ekkor, sem korábban nem hagyja el a félkör alakú pályát, végigcsúszik azon.

A $\displaystyle v_0$ kezdősebességet – $\displaystyle v_1$ ismeretében – a munkatétel alkalmazásával határozhatjuk meg:

$\displaystyle \frac12mv_1^2-\frac12mv_0^2=-2Lmg\mu-2Rmg,$

vagyis

$\displaystyle v_0=\sqrt{\left(\frac{L^2}{4R}+4\mu L+4R\right)g}\approx 8{,}4~\frac{\rm m}{\rm s}.$

Statisztika:

60 dolgozat érkezett.
4 pontot kapott:	Bekes Barnabás, Fekete András Albert, Hamar Dávid, Toronyi András, Varga Vázsony, Vass Bence, Viczián Anna.
3 pontot kapott:	Balázs 825 Ádám , Beke Zsolt, Békési Ábel, Bohács Tamás, Csapó Tamás, Csizy Gergő , Dóra Márton, Endrész Balázs, Fekete Levente, Fiam Regina, Györgyfalvai Fanni, Horváth 999 Anikó, Horváth Antal, Jánosik Áron, Jánosik Máté, Kardkovács Levente, Kertész Balázs, Koczkás József Dániel, Kozák Gergely, Ludányi Levente, Mócza Tamás István, Nagyváradi Dániel, Németh Kristóf, Nguyễn Đức Anh Quân, Nguyen Hoang Trung, Páhán Anita Dalma, Sas 202 Mór, Schäffer Bálint, Schmercz Blanka, Selmi Bálint, Somlán Gellért, Sümegi Géza, Szabados Noémi, Szabó 314 László, Takács Dóra, Tanner Norman, Téglás Panna, Tóth Ábel.
2 pontot kapott:	13 versenyző.
0 pontot kapott:	2 versenyző.

A KöMaL 2020. márciusi fizika feladatai