 |
A P. 5221. feladat (2020. április) |
P. 5221. Egy piciny (pontszerűnek tekinthető) játékautónak építünk egy súrlódásmentes pályát, amely vízszintes szakasszal indul, azután egy \(\displaystyle r\) sugarú, függőleges síkú, kör alakú hurokban folytatódik, majd a hurok kezdetéhez visszaérve ismét vízszintessé válik. Legyen \(\displaystyle v\) az a legkisebb indítási sebesség, amellyel a kisautó már végighalad a pályán. Ezen \(\displaystyle v\) sebesség hányad részével kell elindítani az autót, hogy a hurokszakaszról leválva éppen a kör átellenes pontjába csapódjon majd be?
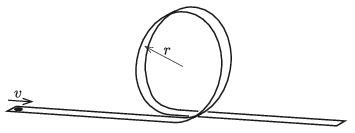
Közli: Vass Miklós, Budapest
(5 pont)
A beküldési határidő 2020. május 11-én LEJÁRT.
Megoldás. A kisautó akkor fut végig a teljes pályán, ha a hurok legmagasabb pontjánál a nehézségi erő éppen fedezni tudja a körmozgáshoz szükséges centripetális erőt. A kocsi sebessége legyen ebben a pontban \(\displaystyle v_1\).
\(\displaystyle mg=\frac{mv_1^2}{r}, \qquad \text{vagyis}\qquad v_1=\sqrt{ gr}.\)
Ahhoz, hogy ekkora sebessége legyen a pálya legmagasabb pontjában, az indítási sebessége (az energiamegmaradás törvénye szerint):
| \(\displaystyle (1)\) | \(\displaystyle v=\sqrt{v_1^2+4gr}= \sqrt{5gr}.\) |
Jelöljük a hurokpályától való elválás helyéhez tartozó, a vízszintestől mért szöget \(\displaystyle \alpha\)-val, a kisautó sebességét pedig ebben a pontban \(\displaystyle v^*\)-gal (lásd az ábrát). A hurokpálya elhagyásának feltétele most is az, hogy a nehézségi erőnek a hurok középpontja felé mutató komponense biztosítani tudja a körmozgáshoz szükséges centripetális erőt:
\(\displaystyle mg\sin\alpha=m\frac{\left(v^*\right)^2}{r},\)
vagyis
| \(\displaystyle (2)\) | \(\displaystyle v^*=\sqrt{gr\sin\alpha}.\) |
A pálya elhagyása után a kisautó ferde hajítással mozog. Kezdősebessége vízszintes irányban \(\displaystyle v^*\sin\alpha\), függőleges irányban pedig \(\displaystyle v^*\cos\alpha\). Ha valamekkora \(\displaystyle t\) idő alatt éppen a pályaelhagyás helyével átellenes pontba érkezik, akkor teljesül:
| \(\displaystyle (3)\) | \(\displaystyle v^*t\sin\alpha=2r\cos\alpha,\) |
illetve
| \(\displaystyle (4)\) | \(\displaystyle \frac{g}{2}\left(v^*\right)^2- v^*t\cos\alpha=2r\sin\alpha.\) |
A \(\displaystyle t\) időt (3)-ból, a \(\displaystyle v^*\) sebességet (2)-ből kifejezve, és ezeket (4)-be helyettesítve kapjuk, hogy
\(\displaystyle \cos^2\alpha=\sin^2\alpha,\qquad \text{vagyis}\qquad \alpha=45^\circ.\)
Ezt (2)-be visszahelyettesítve adódik:
\(\displaystyle v^*=\sqrt{\frac{gr}{\sqrt{2}}}.\)
A kiskocsi indítási sebessége ismét az energiamegmaradás törvényét felhasználva:
\(\displaystyle v'=\sqrt{\left(v^*\right)^2+2gr(1+\sin\alpha)}=\sqrt{gr\left(\frac{1}{\sqrt{2}}+2+ \frac{2}{\sqrt{2}}\right) }.\)
A kérdezett arányszám (1)-t felhasználva:
\(\displaystyle \frac{v'}{v}=\sqrt{\frac{4+3\sqrt2}{10}}\approx 0{,}91.\)
Statisztika:
30 dolgozat érkezett. 5 pontot kapott: Bekes Barnabás, Békési Ábel, Bokor Endre, Fekete András Albert, Fekete Levente, Horváth 999 Anikó, Kertész Balázs, Ludányi Levente, Perényi Barnabás, Selmi Bálint, Somlán Gellért, Szabados Noémi, Toronyi András, Tóth Ábel, Török 111 László, Vass Bence, Viczián Anna. 4 pontot kapott: Schäffer Bálint, Varga Vázsony. 3 pontot kapott: 2 versenyző. 2 pontot kapott: 1 versenyző. 1 pontot kapott: 6 versenyző. 0 pontot kapott: 2 versenyző.
A KöMaL 2020. áprilisi fizika feladatai