A P. 5234. feladat (2020. május)

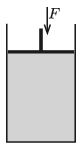
P. 5234. Az ábra szerinti, függőleges szimmetriatengelyű, hengeres tartályt felül egy súlytalannak tekinthető dugattyú zár el. A 7 dm$\displaystyle {}^3$ térfogatú edényben nincs levegő, csak $\displaystyle T$ hőmérsékletű, telített vízgőzt tartalmaz. Mekkora munkát végzünk, ha a dugattyút lassan addig nyomjuk le, míg az folyadékba nem ütközik? A folyamat során az egész rendszer hőmérséklete állandó. Számítsuk ki és ábrázoljuk a végzett munkát a $\displaystyle T$ hőmérséklet függvényében, ahol $\displaystyle 100\;{}^\circ\mathrm{C}\le T\le 370\;{}^\circ\mathrm{C}$. (A telített vízgőz nyomására, sűrűségére és a víz sűrűségére vonatkozó adatokat vegyük a Négyjegyű függvénytáblázatokból!)

Közli: Légrádi Imre, Sopron

(4 pont)

A beküldési határidő 2020. június 10-én LEJÁRT.

Megoldás. Az $\displaystyle A$ keresztmetszetű dugattyút felülről $\displaystyle p_0A$ erővel nyomja a külső légnyomás lefelé ($\displaystyle p_0=101~\rm kPa$), alulról pedig a gőz $\displaystyle p_\text{gőz}A$ erővel felfelé. Állandó hőmérsékleten a gőznyomás állandó, tehát a (súlytalan) dugattyú lenyomásához állandó

$\displaystyle F=\left(p_\text{gőz}-p_0\right)A$

erőt kell kifejtenünk.

Az eredeti $\displaystyle V_0$ térfogatban $\displaystyle m=\varrho_\text{gőz}V_0$ tömegű vízgőz található. A teljes gőzmennyiség lecsapódásakor a térfogat

$\displaystyle V_1=\frac{m}{\varrho_\text{víz}}=\frac{\varrho_\text{gőz}}{\varrho_\text{víz}}V_0$

értékre csökken, a dugattyú elmozdulása tehát

$\displaystyle \Delta x=\frac{V_0-V_1}{A},$

az általunk végzett munka pedig

$\displaystyle W=F\Delta x=\left(p_\text{gőz}-p_0\right)\left(1-\frac{\varrho_\text{gőz}}{\varrho_\text{víz}}\right) V_0.$

Ebben a képletben $\displaystyle \varrho_\text{gőz}$, $\displaystyle \varrho_\text{víz}$ és $\displaystyle p_\text{gőz}$ a hőmérséklet szerint változó mennyiségek, nagyságukat pl. a Négyjegyű függvénytáblázatokban találhatjuk meg. Feltételezve, hogy $\displaystyle p_0=101$ kPa, az ábrán vázolt grafikonnak megfelelő $\displaystyle W(T)$ értékeket kapjuk:

Látható, hogy a függvénykapcsolat nem monoton, hanem kb. $\displaystyle T_0=350~^\circ\rm C$-nál maximuma van. Eszerint előfordulhat, hogy két különböző hőmérsékletnél a vízgőz összenyomásakor végzett munka ugyanakkora. A hőmérséklet növelésekor a vízgőz nyomása ugyan fokozatosan nő (és emiatt egyre nagyobb erővel lehet csak lenyomni a dugattyút), azonban a gőz és a víz sűrűségének aránya is egyre növekszik. Így nagyobb erőt kisebb úton kell kifejtenünk, emiatt előfordulhat, hogy magasabb hőmérsékleten kisebb lesz a szükséges munkavégzés, mint egy alacsonyabb hőmérsékletnél.

Statisztika:

3 dolgozat érkezett.
4 pontot kapott:	Ludányi Levente.
3 pontot kapott:	Sas 202 Mór.
0 pontot kapott:	1 versenyző.

A KöMaL 2020. májusi fizika feladatai