 |
A P. 5236. feladat (2020. május) |
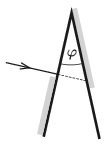
P. 5236. Egy üvegprizma egyik lapjára merőlegesen esik egy fénysugár, amely a prizma másik oldalán, felül még nem tud kilépni, mert az a rész tükröző anyaggal van bevonva. A prizma első oldalát a belépési pont alatt ugyancsak tükröző anyaggal vonták be, ezért a fény ezen a részen sem tud kilépni az üvegből, hanem visszaverődik. Végül a túlsó oldalon kilépő fénysugár a prizmához érkező fénysugár irányához képest 40∘-kal térül el. Mekkora a prizma törőszöge, ha az anyagának törésmutatója 1,5?
Közli: Zsigri Ferenc, Budapest
(4 pont)
A beküldési határidő 2020. június 10-én LEJÁRT.
Megoldás. Ha a prizma törőszöge φ, akkor a fénysugár útja mentén az egymást követő beesési szögek: nulla, φ, 2φ, végül 3φ (lásd az ábrát). A prizmából kilépő fénysugár törési szöge, ha a megadott feltétel teljesül, 40∘+φ.

A fénytörés törvénye szerint fennáll:
sin(40∘+φ)=1,5sin(3φ).
Ezt az egyenlet numerikusan (próbálkozással, fokozatosan behatárolva a gyökét) meg lehet oldani. Első közelítésben, ha az egyenletben szereplő szögek szinuszát magával a (radiánban kifejezett) szöggel helyettesítjük, a φ≈80∘/7≈11∘ értéket kapjuk. Ezt – akár egy zsebszámológéppel – tovább finomíthatjuk, így a prizma keresett törőszögére végül a
φ≈10,3∘
eredmény adódik.
Statisztika:
30 dolgozat érkezett. 4 pontot kapott: Bagu Bálint, Balázs 825 Ádám , Bekes Barnabás, Endrész Balázs, Fekete András Albert, Fekete Levente, Györgyfalvai Fanni, Horváth 999 Anikó, Kardkovács Levente, Kozák Gergely, Ludányi Levente, Mócza Tamás István, Németh Kristóf, Nguyễn Đức Anh Quân, Perényi Barnabás, Sas 202 Mór, Selmi Bálint, Somlán Gellért, Szabados Noémi, Szász Levente, Tanner Norman, Toronyi András, Török 111 László, Varga Vázsony, Vass Bence. 3 pontot kapott: Hamar Dávid. 2 pontot kapott: 3 versenyző. Nem számítjuk a versenybe a születési dátum vagy a szülői nyilatkozat hiánya miatt: 1 dolgozat.
A KöMaL 2020. májusi fizika feladatai
|
|

