 |
A P. 5251. feladat (2020. október) |
P. 5251. Az \(\displaystyle m\) tömegű, kis méretű testet az ábrán látható, rögzített hasáb \(\displaystyle A\) pontjában kezdősebesség nélkül elengedjük. A test a bal oldali egyenes szakaszon és az \(\displaystyle R\) sugarú köríven súrlódásmentesen csúszik. A jobb oldali egyenes szakasz nem súrlódásmentes, a súrlódási tényező \(\displaystyle \mu\).
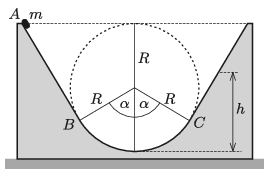
\(\displaystyle a)\) Mekkora erővel nyomja a test a hasábot a pálya legmélyebb pontján?
\(\displaystyle b)\) Mekkora a test sebessége a \(\displaystyle C\) pontban?
\(\displaystyle c)\) Milyen \(\displaystyle h\) magasságba emelkedik fel a test?
Adatok: \(\displaystyle m =0{,}6\) kg, \(\displaystyle R = 30\) cm, \(\displaystyle \alpha = 60^\circ\), \(\displaystyle \mu = \frac12 \tg\alpha\).
Közli: Kotek László, Pécs
(5 pont)
A beküldési határidő 2020. november 16-án LEJÁRT.
Megoldás. \(\displaystyle a)\) Jelöljük a keresett sebességet \(\displaystyle v\)-vel, és írjuk fel a munkatételt az \(\displaystyle A\) pont és a pálya legmélyebb pontja közötti mozgásra:
\(\displaystyle mg\cdot 2R=\frac{1}{2}mv^2,\)
vagyis
\(\displaystyle \frac{v^2}{R}=4g.\)
(Ez a mennyiség nem más, mint a test centripetális gyorsulása a pálya legmélyebb pontjánál.) A dinamika alaptörvénye szerint
\(\displaystyle N-mg=4mg,\)
azaz a hasábotot nyomó erő:
\(\displaystyle N=5mg=29{,}4~{\rm N}.\)
\(\displaystyle b)\) Jelöljük a kérdéses sebességet \(\displaystyle u\)-val, és írjuk fel a munkatételt az \(\displaystyle A\) és a \(\displaystyle C\) pont közötti mozgásra:
\(\displaystyle mg(R+R\cos\alpha)=\frac{mu^2}{2},\)
tehát
\(\displaystyle u=\sqrt{2g(R+R\cos\alpha)}=\sqrt{3Rg}=2{,}97~\frac{\rm m}{\rm s}\approx 3~\frac{\rm m}{\rm s}.\)
\(\displaystyle c)\) Legyen a súrlódásos szakasz hossza \(\displaystyle \ell\). Mivel a testre ható súrlódási erő \(\displaystyle S=mg\mu \cos\alpha=\frac{mg}{2}\sin\alpha\), a munkatétel az indulástól a megállásig:
\(\displaystyle mg\left(\frac32R-\ell\sin\alpha\right)- \frac{mg}{2}\ell\sin\alpha =0,\)
ahonnan \(\displaystyle \ell\sin\alpha=R\) következik. A kérdéses magasság tehát
\(\displaystyle h=R(1-\cos\alpha)+\ell\sin\alpha = R\left(1-\frac12\right)+R=\frac32R=45~\rm cm.\)
Statisztika:
91 dolgozat érkezett. 5 pontot kapott: Antalóczy Szabolcs, Balogh Huba Kadosa, Bognár 171 András Károly, Bonifert Balázs, Csapó Tamás, Csonka Illés, Dobre Zsombor, Domján Dorina, Dóra Márton, Ferencz Kamilla, Gurzó József, Juhász Júlia, Kaltenecker Balázs Bence, Kertész Balázs, Koleszár Benedek, Koszta Benedek, Kovács Kinga, Kozaróczy Csaba, Köpenczei Csanád, Ludányi Levente, Mócza Tamás István, Mozolai Bende Bruno, Németh Kristóf, Perényi Barnabás, Répási Tamás, Ruzsa Bence, Sas 202 Mór, Schäffer Bálint, Schmercz Blanka, Somlán Gellért, Somogyi Boglárka Zsófia, Surányi Blanka, Szabó Márton, Szász Levente, Szirmai Dénes, Szoboszlai Szilveszter, Téglás Panna, Toronyi András, Tóth Ábel, Török 111 László, Török Dorka, Varga Vázsony, Viczián Máté. 4 pontot kapott: 16 versenyző. 3 pontot kapott: 15 versenyző. 2 pontot kapott: 6 versenyző. 1 pontot kapott: 5 versenyző. 0 pontot kapott: 5 versenyző. Nem versenyszerű: 1 dolgozat.
A KöMaL 2020. októberi fizika feladatai