 |
A P. 5252. feladat (2020. október) |
P. 5252. \(\displaystyle M\) tömegű, vékony falú csőre fonalat csévélünk, és a fonalat húzva az ábrán látható módon a csövet állandó sebességgel gurítjuk. A cső tisztán gördül a vízszintes talajon. A cső belsejébe kis méretű, \(\displaystyle m\) tömegű testet helyeztünk, ami odabent állandósult szöghelyzetben csúszik, a súrlódási együttható itt \(\displaystyle \mu\). Mekkora vízszintes fonálerő szükséges az állandó sebesség fenntartásához?
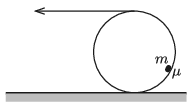
Közli: Vladár Károly, Kiskunhalas
(5 pont)
A beküldési határidő 2020. november 16-án LEJÁRT.
Megoldás. Használjuk az ábra jelöléseit, és írjuk le a mozgást a cső tengelyével együtt mozgó koordináta-rendszerben.
Az \(\displaystyle m\) tömegű test (a stacionárius állapot beállta után) nem mozog, miközben alatta egy \(\displaystyle \alpha\) hajlásszögű ,,lejtő'' csúszik felfelé. Az erőegyensúly feltétele: \(\displaystyle \alpha\) éppen a súrlódási határszöggel egyezik meg, vagyis
\(\displaystyle \mu=\tg\alpha.\)
A karika egyenletesen forog, ezért a rá ható erők eredő forgatónyomatéka tetszőleges pontra, pl. a talajjal érintkező pontjára vonatkoztatva nulla. Erre a pontra nézve csak a fonalat feszítő \(\displaystyle F\) nagyságú, vízszintes erőnek és az \(\displaystyle mg\) nagyságú nehézségi erőnek van forgatónyomatéka.
A forgatónyomatékok egyensúlyának feltétele:
\(\displaystyle mgR\sin\alpha=2RF,\)
vagyis
\(\displaystyle F=\frac{mg}{2}\sin\alpha=\frac{mg}{2}\frac{\tg\alpha}{\sqrt{1+\tg^2\alpha}} =\frac{mg}{2}\frac{\mu}{\sqrt{1+\mu^2}}.\)
Megjegyzés. Látható, hogy a szükséges fonálerő nem függ a cső \(\displaystyle M\) tömegétől.
Statisztika:
39 dolgozat érkezett. 5 pontot kapott: Barkóczi Zsombor , Bognár 171 András Károly, Bonifert Balázs, Fekete András Albert, Gurzó József, Horváth 999 Anikó, Kertész Balázs, Koszta Benedek, Kovács Kinga, Ludányi Levente, Selmi Bálint, Somlán Gellért, Takács Bendegúz, Téglás Panna, Toronyi András, Tóth Ábel, Török 111 László, Varga Vázsony. 4 pontot kapott: Kozaróczy Csaba, Molnár 123 Barnabás, Sas 202 Mór. 3 pontot kapott: 10 versenyző. 2 pontot kapott: 2 versenyző. 1 pontot kapott: 4 versenyző. 0 pontot kapott: 1 versenyző. Nem versenyszerű: 1 dolgozat.
A KöMaL 2020. októberi fizika feladatai