A P. 5268. feladat (2020. november)

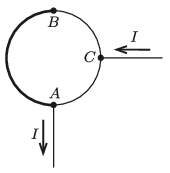
P. 5268. Egy $\displaystyle d_1 = 3$ mm és egy $\displaystyle d_2 = 1{,}5$ mm átmérőjű rézvezetéket úgy forrasztunk össze, hogy az egyes vezetékdarabok félköröket alkotva $\displaystyle r = 4$ cm sugarú körré egészítsék ki egymást. A zárt kör egyik forrasztási pontjához $\displaystyle (A)$ és a vékonyabbik huzalból készült félkör felezőpontjához $\displaystyle (C)$ egy-egy igen hosszú egyenes vezeték csatlakozik. Határozzuk meg a körvezető középpontjában a mágneses mező indukcióvektorát, ha a csatlakozó vezetékekben $\displaystyle I = 25$ A erősségű áram folyik!

Közli: Holics László, Budapest

(4 pont)

A beküldési határidő 2020. december 15-én LEJÁRT.

Megoldás. Jelöljük a vékonyabb huzal negyedkörének ellenállását $\displaystyle 2R$-rel. A vastagabb huzal keresztmetszete négyszer nagyobb, mint a vékonyabbé, hosszegységre jutó ellenállása tehát négyszer kisebb. A félkör hossza kétszerese a negyedkörének, az ellenállása tehát $\displaystyle 2\cdot \tfrac14\cdot 2R=R$.

Az $\displaystyle I=25$ A erősségű áram $\displaystyle 2:3$ arányban oszlik meg a $\displaystyle 3R$ ellenállású $\displaystyle CBA$ ág és a $\displaystyle 2R$ ellenállású $\displaystyle CA$ ág között. A hosszabb vezetékdarabban tehát $\displaystyle \tfrac25 I=10$ A, a rövidebb darabban pedig $\displaystyle \tfrac35 I=15$ A erősségű áram folyik.

Egy $\displaystyle r$ sugarú, $\displaystyle I$ erősségű árammal átjárt körvezető középpontjában $\displaystyle B=\mu_0\frac{I}{2r}$ a mágneses indukció, a körívek keltette mágneses indukció nagysága az ívek hosszával arányosan kevesebb. Az egyik ágban folyó áram tehát

$\displaystyle B_1= \mu_0\frac{I}{2r}\cdot \frac34\cdot \frac25,$

a másik pedig

$\displaystyle B_2= \mu_0\frac{I}{2r}\cdot \frac14\cdot\frac35$

nagyságú indukcióvektort hoz létre. Ezek egymással ellentétes irányúak, így az eredő nagysága

$\displaystyle B=B_1-B_2=\frac3{40}\,\frac{\mu_0 I}{r}=5{,}89\cdot 10^{-5}~\rm T.$

Statisztika:

25 dolgozat érkezett.
4 pontot kapott:	Antalóczy Szabolcs, Beke Zsolt, Biebel Botond, Fonyi Máté Sándor, Horváth 999 Anikó, Kozák Gergely, Lévay Kristóf, Ludányi Levente, Mozolai Bende Bruno, Selmi Bálint, Somlán Gellért, Strinyi Péter, Takács Bendegúz, Téglás Panna, Toronyi András, Tóth Ábel.
3 pontot kapott:	Gál Virág , Gurzó József, Hauber Henrik, Magyar Gábor Balázs, Nagyváradi Dániel, Puskás Attila, Tuba Balázs.
1 pontot kapott:	2 versenyző.

A KöMaL 2020. novemberi fizika feladatai