A P. 5272. feladat (2020. december)

P. 5272. Az ábrán látható négy belső fogaskerék körbejár, a külső pedig áll. (A fogaskerekek mozgása a honlapon megtekinthető.)

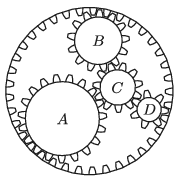
Mekkora az \(\displaystyle A\), \(\displaystyle B\) és \(\displaystyle C\) jelű fogaskerék fordulatszáma, ha a legkisebb, \(\displaystyle D\) jelű fogaskerék másodpercenként egyszer fordul körbe?

Közli: Baranyai Klára, Veresegyház

(5 pont)

A beküldési határidő 2021. január 15-én LEJÁRT.

I. megoldás. Az ábráról leolvashatjuk, hogy a külső (álló) fogaskerék fogainak száma \(\displaystyle n_0=37\), a belső fogaskerekeké pedig

\(\displaystyle n_A=19; \qquad n_B=13; \qquad n_C=11; \qquad n_D=7.\)

Gondolatban egyenesítsük ki a 37 fogú külső kereket, így egy 37 fogú fogaslécet kapunk, majd ezen vezessük végig az \(\displaystyle A\), a \(\displaystyle B\) és a \(\displaystyle D\) jelű fogaskerekeket. Megállapíthatjuk, hogy ezek rendre \(\displaystyle \tfrac{37}{19}\), \(\displaystyle \tfrac{37}{13}\) és \(\displaystyle \tfrac{37}{7}\) fordulatot végeznek. Ha visszatérünk a fogaslécről az eredei (kör alakú) fogaskerékre, akkor a mozgó kerekek körülfordulásának száma a fenti értékeknél minden esetben eggyel kisebb lesz. Ezt úgy láthatjuk be, ha gondolatban az álló fogaslécen lépünk egy foggal előrébb (a görgetett kerékkel együtt, annak mozgásirányába), majd a fogaslécen annyit hajlítunk visszafelé, hogy végül kialakuljon a teljes kör. A fogasléc visszahajlításakor a rajta lévő fogaskerék is visszafelé fordul el. A sok kis visszafordulás végül egy teljes körré áll össze, ezért kell egyet levonnunk az egyenes fogaslécnél kiszámolt értékből.

Tehát miközben a belső fogaskerekek először visszatérnek eredeti helyzetükbe, az \(\displaystyle A\), \(\displaystyle B\) és \(\displaystyle D\) kerekek rendre

\(\displaystyle \frac{37}{19}-1=\frac{18}{19};\qquad \frac{37}{13}-1=\frac{24}{13}; \qquad \frac{37}{7}-1=\frac{30}{7}\)

fordulatot végeznek. Ha a legkisebb fogaskerék másodpercenként egyet fordul, akkor a teljes körülforduláshoz 30/7 másodperc szükséges. Így megkaphatjuk az \(\displaystyle A\) és a \(\displaystyle B\) jelű fogaskerekek fordulatszámát:

\(\displaystyle f_A=\frac{ {18}/{19}} { {30}/{7}} ~{\rm s}^{-1}=\frac{21}{95}~{\rm s}^{-1}=0{,}221~{\rm s}^{-1}; \qquad f_B=\frac{ {24}/{13}} { {30}/{7}}~{\rm s}^{-1}=\frac{28}{65}~{\rm s}^{-1}=0{,}431~{\rm s}^{-1}.\)

Hátra van még a 11 fogú, \(\displaystyle C\) jelű fogaskerék. Ezt ugyanolyan gyorsan (de visszafelé, a fogasléc folyamatos meggörbítésével megegyező irényba) hajtja mind a három másik kerék, ezért \(\displaystyle C\) fordulatszámát akár háromféleképpen is kiszámíthatjuk. Egy teljes körüljárás alatt a kerék körülfordulásainak száma:

\(\displaystyle \frac{37/19}{11/19}+1=\frac{37/13}{11/13}+1=\frac{37/7}{11/7}+1= \frac{37 }{11}+1=\frac{48}{11}.\)

Az előzőekhez hasonlóan végül a \(\displaystyle C\) jelű fogaskerék fordulatszáma:

\(\displaystyle f_C=\frac{ {48}/{11}} { {30}/{7}} ~{\rm s}^{-1}=\frac{56}{55}~{\rm s}^{-1}=1{,}018~{\rm s}^{-1},\)

forgásának iránya pedig a többiekével ellentétes.

II. megoldás. Az ábráról leolvashatjuk, hogy a külső (álló) fogaskerék fogainak száma \(\displaystyle n_0=37\), a belső fogaskerekeké pedig

\(\displaystyle n_A=19; \qquad n_B=13; \qquad n_C=11; \qquad n_D=7.\)

Jelöljük a belső fogaskerekek (azok mozgó tengelyeinek) keringési fordulatszámát \(\displaystyle f_0\)-lal.

Üljünk bele egy olyan \(\displaystyle \cal K'\) koordináta-rendszerbe, amely együtt forog a tengelyekkel, vagyis a fordulatszáma az eredeti, az álló külső kerékhez rögzített \(\displaystyle \cal K\) koordináta-rendszerben éppen \(\displaystyle f_0\). Ebből a rendszerből nézve a négy belső fogaskerék tengelye áll, a külső kerék pedig \(\displaystyle f_0\) fordulatszámmal forog az óramutató járásával megegyező irányban.

A belső kerekek fordulatszáma a \(\displaystyle \cal K'\) rendszerben (a fogak számának arányában)

\(\displaystyle f'_A= \frac{37}{19}f_0; \qquad f'_B= \frac{37}{13}f_0; \qquad -f'_C= \frac{37}{19}\cdot \frac{19}{11}f_0= \frac{37}{13}\cdot\frac{13}{11}f_0= \frac{37}{7}\cdot\frac{7}{11}f_0=\frac{37}{11}f_0; \qquad f'_D= \frac{37}{7}f_0. \)

(\(\displaystyle f'_C\) képletében a negatív előjel azt fejezi ki, hogy ez a fogaskerék a másik hárommal ellentétes irányban forog.)

Az eredeti \(\displaystyle \cal K\) rendszerbe úgy térhetünk vissza, hogy a fordulatszámokból levonjuk a két rendszer egymáshoz képesti forgásának \(\displaystyle f_0\) fordulatszámát:

\(\displaystyle f_A=f'_A-f_0=\frac{18}{19}f_0; \quad f_B= f'_B-f_0=\frac{24}{13}f_0;\quad f_C=f'_C-f_0= -\frac{48}{11}f_0;\quad f_D=f'_D-f_0= \frac{30}{7}f_0.\)

Tudjuk, hogy

\(\displaystyle f_D=1~\rm s^{-1},\qquad \text{vagyis}\qquad f_0=\frac{7}{30}~\rm s^{-1}.\)

Innen következik, hogy a körbejáró fogaskerekek másodpercenkénti fordulatszáma

\(\displaystyle f_A=\frac{21}{95}\approx 0{,}22;\qquad f_B=\frac{28}{65}\approx 0{,}43;\qquad f_C=-\frac{56}{55}\approx -1{,}02.\)

Statisztika:

58 dolgozat érkezett.
5 pontot kapott:	Fekete András Albert, Koleszár Benedek, Kozaróczy Csaba, Sas 202 Mór, Téglás Panna.
4 pontot kapott:	Fey Dávid, Horváth Antal, Kovács Kinga, Ludányi Levente, Tóth Ábel, Török 111 László, Varga Vázsony.
3 pontot kapott:	2 versenyző.
2 pontot kapott:	31 versenyző.
1 pontot kapott:	11 versenyző.
0 pontot kapott:	2 versenyző.

A KöMaL 2020. decemberi fizika feladatai