 |
A P. 5273. feladat (2020. december) |
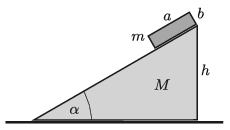
P. 5273. Az ábrán látható, vízszintes síkon elhelyezett, \(\displaystyle \alpha= 30^\circ\)-os, \(\displaystyle M = 1\) kg tömegű, \(\displaystyle h = 60\) cm magasságú derékszögű lejtő tetején nyugvó \(\displaystyle m = 0{,}5\) kg tömegű, \(\displaystyle a = 20\) cm alapú, \(\displaystyle b = 10\) cm magasságú téglatestet kezdetben nyugalomban tartjuk. Egy adott pillanatban a téglatestet elengedjük. A súrlódás mindenütt elhanyagolható.
\(\displaystyle a)\) Mekkora a két test sebességének nagysága, amikor a téglatest a talajhoz ér?
\(\displaystyle b)\) Mennyi idő alatt jut el a tégla a talajhoz?
\(\displaystyle c)\) Mekkora utat tesz meg ezalatt a téglatest?
Közli: Holics László, Budapest
(5 pont)
A beküldési határidő 2021. január 15-én LEJÁRT.
I. megoldás. Jelöljük a gyorsulásokat és a erőket az ábrán látható módon.
A lejtő mozgásegyenlete:
| \(\displaystyle (1)\) | \(\displaystyle MA=N\,\sin\alpha.\) |
Ha a lecsúszó téglatest vízszintes irányú gyorsulása (a talajhoz képest) \(\displaystyle a_1\), a függőleges gyorsulása pedig \(\displaystyle a_2\), akkor a mozgásegyenletei:
| \(\displaystyle (2)\) | \(\displaystyle N \sin\alpha=ma_1,\) |
illetve
| \(\displaystyle (3)\) | \(\displaystyle mg-N\cos\alpha=ma_2.\) |
A téglatest mindvégig a lejtőn marad, ennek feltétele:
| \(\displaystyle (4)\) | \(\displaystyle a_2=\left(a_1+A\right)\tg\alpha.\) |
Az (1)-(4) egyenletrendszer megoldása:
\(\displaystyle A=\frac{m\sin\alpha\cos\alpha}{m\sin^2\alpha+M}\,g=1{,}89~ \frac{\rm m}{s^2},\)
\(\displaystyle a_1=\frac{M\sin\alpha\cos\alpha}{M+m\sin^2\alpha}\,g=3{,}78~ \frac{\rm m}{ s^2},\)
\(\displaystyle a_2= \frac{(M+m)\sin^2\alpha}{M+m\sin^2\alpha}\,g=3{,}27~ \frac{\rm m}{ s^2},\)
és végül
\(\displaystyle N=\frac{M \cos\alpha}{M+m\sin^2\alpha}\,mg=3{,}78~ \rm N.\)
\(\displaystyle b)\) Függőleges irányban a téglatest \(\displaystyle s=h-a\sin\alpha=0{,}5~\rm m\)-t mozdul el. A mozgás ideje:
\(\displaystyle t=\sqrt{\frac{2s}{a_2}}=0{,}55~\rm s.\)
\(\displaystyle a)\) A lejtő sebessége a kérdéses pillanatban:
\(\displaystyle V^{\rm (max)}=At=1{,}04~\frac{\rm m}{\rm s},\)
míg a lejtőn csúszó téglatest legnagyobb sebességének komponensei:
\(\displaystyle v_{1\rm max}=a_1t=2{,}08~\frac{\rm m}{\rm s},\qquad v_{2\rm max}=a_2t=1{,}81~\frac{\rm m}{\rm s},\)
a sebességének nagysága tehát
\(\displaystyle v=\sqrt{v_{1\rm max}^2+v_{2\rm max}^2}=2{,}76~\frac{\rm m}{\rm s}.\)
\(\displaystyle c)\) A téglatest elmozdulásvektorának komponensei:
\(\displaystyle s_1=\frac{a_1}{2}t^2=0{,}57~{\rm m}; \qquad s_2=\frac{a_2}{2}t^2=0{,}67~{\rm m}=0{,}5~{\rm m},\)
az elmozdulás nagysága (vagyis a megtett útja):
\(\displaystyle \ell=\sqrt{s_1^2+s_2^2}=0{,}76~\rm m.\)
II. megoldás. A feladatot az energia- és a lendületmegmaradás tételének alkalmazásával is meg lehet oldani.
Jelöljük a lejtő gyorsulását \(\displaystyle A\)-val, a téglatestnek a lejtőhöz viszonyított gyorsulását pedig \(\displaystyle a_0\)-lal! A lecsúszás \(\displaystyle t\) ideje alatt a megfelelő sebességek: \(\displaystyle V=At\) és \(\displaystyle v_0=a_0t\).
A téglatest sebességének vízszintes komponense a talajhoz képest
\(\displaystyle v_1=a_0t\cos\alpha-At,\)
a sebesség nagysága pedig (ismét a talajhoz viszonyítva) a koszinusz-tételt alkalmazásával:
| \(\displaystyle (5)\) | \(\displaystyle u=\sqrt{v_0^2+V^2-2v_0V\cos\alpha}=t\sqrt{a_0^2+A^2-2a_0A\cos\alpha}.\) |
A lendületmegmaradás tétele szerint
\(\displaystyle MAt=m\left(a_0\cos\alpha-A\right)t,\)
vagyis
| \(\displaystyle (6)\) | \(\displaystyle a_0=\frac{m+M}{m}\frac{1}{\cos\alpha}A.\) |
A téglatest \(\displaystyle t\) idő alatt érkezik \(\displaystyle \frac h{\sin\alpha}-a=1~\)m-t megtéve lejtő aljára, vagyis
| \(\displaystyle (7)\) | \(\displaystyle \frac h{\sin\alpha}-a=\frac{a_0}{2}t^2.\) |
Az energiamegmaradás tétele szerint
\(\displaystyle \frac{1}{2}MV^2+\frac{1}{2}mu^2=mgh,\)
tehát
\(\displaystyle \frac{1}{2}M(At)^2+\frac{1}{2}m\left( a_0^2+A^2-2a_0A\cos\alpha \right)t^2=mg\frac{a_0}{2}t^2\,\sin\alpha.\)
Innen egyszerűsítések és (6) felhasználása után az
\(\displaystyle MA^2+m\left(A^2+\frac{(M+m)^2}{m^2\cos^2\alpha}A^2-2A^2\frac{ M+m }{m}\right)= (M+m)gA \frac{\sin\alpha}{\cos\alpha},\)
vagyis az
\(\displaystyle A=\frac{\sin\alpha\,\cos\alpha}{(M/m)+\sin^2\alpha}g=1{,}89~ \frac{\rm m}{s^2}\)
eredményt kapjuk. Innen (6) szerint
| \(\displaystyle (8)\) | \(\displaystyle a_0= \frac{\sin\alpha }{(M/m)+\sin^2\alpha}\left(1+\frac Mm\right)g=6{,}54~ \frac{\rm m}{s^2}.\) |
\(\displaystyle b)\) A csúszás ideje (7) alapján
\(\displaystyle t=\sqrt{ \frac2{a_0}\left({\frac h{\sin\alpha}-a}\right)}=0{,}55~\rm s.\)
\(\displaystyle a)\) A lejtő sebessége a téglatest leérkezésekor
\(\displaystyle V=At=1{,}04~\frac{\rm m }{\rm s},\)
a téglatest sebessége pedig (\(\displaystyle a_0t=3{,}60~\rm m/s\) ismeretében) (5) szerint
\(\displaystyle u=\sqrt{3{,}60^2+1{,}04^2-2\cdot3{,}60\cdot1{,}04\cdot\cos 30^\circ }~\frac{\rm m }{\rm s}=2{,}75~\frac{\rm m }{\rm s}. \)
\(\displaystyle c)\) A téglatest (a talajhoz képest)
\(\displaystyle \ell=\frac{u}{2}t=0{,}76~\rm m\)
utat tesz meg.
Statisztika:
56 dolgozat érkezett. 5 pontot kapott: Csapó Tamás, Fey Dávid, Gurzó József, Kertész Balázs, Koleszár Benedek, Somlán Gellért, Toronyi András, Varga Vázsony, Viczián Máté. 4 pontot kapott: Biebel Botond, Bubics Gergely Dániel, Horváth 999 Anikó, Kozaróczy Csaba, Ludányi Levente, Téglás Panna, Tóth Ábel, Török 111 László. 3 pontot kapott: 8 versenyző. 2 pontot kapott: 16 versenyző. 1 pontot kapott: 6 versenyző. 0 pontot kapott: 7 versenyző. Nem versenyszerű: 2 dolgozat.
A KöMaL 2020. decemberi fizika feladatai