A P. 5279. feladat (2020. december)

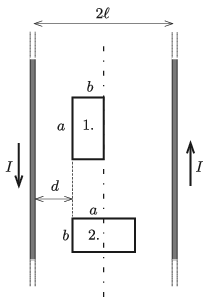
P. 5279. Két nagyon hosszú, egymástól $\displaystyle 2\ell$ távol lévő egyenes vezető huzal mindegyikében $\displaystyle I$ erősségű, de ellentétes irányú áram folyik. A vezetők síkjában, az egyik vezetőtől $\displaystyle d=\ell-b$ távolságban egy $\displaystyle a$ és $\displaystyle b$ oldalhosszúságú téglalap alakú vezetőkeretet helyeztünk el, először az ábrán látható 1-es, majd a 2-es helyzetben ($\displaystyle 0<a-b<\ell)$. Melyik esetben nagyobb a kereten átmenő mágneses fluxus?

Cserti József (Budapest) feladata nyomán

(4 pont)

A beküldési határidő 2021. január 15-én LEJÁRT.

Megoldás. A két áram mágneses tere a két vezető között erősíti egymást. Tudjuk, hogy egyetlen hosszú vezetőtől $\displaystyle \ell-x$ távolságban az indukció $\displaystyle \frac{1}{\ell-x}$-szel arányos, a két vezető áramának eredő tere pedig a szimmetriatengelytől $\displaystyle x$ távolságban (egyforma áramerősségek esetén)

$\displaystyle \frac{1}{\ell-x}+\frac{1}{\ell+x}=\frac{2\ell}{\ell^2-x^2}$

kifejezéssel arányos. Látható, hogy az indukcióvektor nagysága a szimmetriatengely mentén a legkisebb, onnan bármelyik irányba elmozdulva $\displaystyle B(x)$ növekszik

A kétféle esetet összehasonlítva az ábra alapján megállapíthatjuk, hogy a sötétebben jelölt négyzeteken átmenő fluxus megegyezik.

A maradék fehér téglalapok közül $\displaystyle a>2b$ esetén az 1-es helyzetben kisebb a fluxus (hiszen a két téglalap területe megegyezik, és a bal oldali téglalap bármelyik pontjánál $\displaystyle B$ kisebb, mint amekkora a jobb oldali téglalap bármelyik pontjánál $\displaystyle B$ nagysága.) Emiatt ilyenkor $\displaystyle \Phi_1<\Phi_2$.

$\displaystyle a<2b$ esetén éppen fordított a helyzet, tehát ilyenkor $\displaystyle \Phi_2<\Phi_1$, ha pedig $\displaystyle a=2b$, akkor a fluxus mindkét helyzetben ugyanakkora.

Statisztika:

15 dolgozat érkezett.
4 pontot kapott:	Mihalik Bálint, Páhán Anita Dalma, Somlán Gellért, Téglás Panna, Tóth Ábel.
3 pontot kapott:	Beke Zsolt, Kertész Balázs.
2 pontot kapott:	2 versenyző.
1 pontot kapott:	2 versenyző.
0 pontot kapott:	4 versenyző.

A KöMaL 2020. decemberi fizika feladatai