 |
A P. 5286. feladat (2021. január) |
P. 5286. Egy R sugarú, homogén tömegeloszlású, φ szöggel ,,hiányos'' vékony hengerpalástot vízszintes asztalra fektetünk az ábrán látható módon. A hengerpalástot kissé kimozdítjuk egyensúlyi helyzetéből, majd elengedjük. Határozzuk meg a hengerpalást rezgőmozgásának periódusidejét! Feltételezhetjük, hogy súrlódás elegendően nagy, így a hengerpalást a rezgőmozgás közben nem csúszik meg.
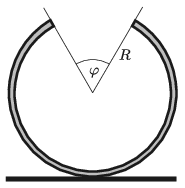
Adatok: R=0,2 m; φ=π/3.
Közli: Takács Árpád, Budapesti Berzsenyi D. Gimn.
(5 pont)
A beküldési határidő 2021. február 18-án LEJÁRT.
I. megoldás. Táblázati adatok szerint a hiányos hengerpalást tömegközéppontja d=Rsinδδ távolságban van a henger tengelyétól, ahol δ=π−φ2. (Lásd pl. a Négyjegyű függvénytáblázatokban a Homogén tömegeloszlású vonalas alakzatok tömegközéppontja c. részt.) Esetünkben δ=5π/6, tehát d=0,191R=3,82 cm.
A hiányos hengerpalástnak az O tengelyére vonatkoztatott tehetetlenségi nyomatéka ΘO=mR2, hiszen minden darabkája R távol van az O tengelytől. Eszerint a T tömegközépponton átmenő tengelyre vonatkozó tehetetlenségi nyomaték (a Steiner-tétel szerint)
ΘT=ΘO−md2=m(R2−d2).
Írjuk fel az a≪1 szöggel kitérített test mozgásegyenleteit és a csúszásmentes gördülés kényszerfeltételét.
ΘTβ=−mgdsinα−S(R−dcosα),
S=ma,
(R−d)β=a.
Itt S a korongra ható (tapadó) súrlódási erő, a a tömegközéppont vízszintes irányú gyorsulása, β pedig a szöggyorsulás. A függőleges irányú gyorsulás nagyon (másodrendűen) kicsi, emiatt az asztal által kifejtett nyomóerő mg-nek vehető (1. ábra).

1. ábra
S és a kiküszöbölése után (a sinα≈α valamint a cosα≈1 közelítést alkalmazva) kapjuk, hogy
(ΘT+m(R−d)2)β=−mgd⋅α,
vagyis
β=−K⋅α,
ahol K egy állandó. Ez egy olyan harmonikus rezgőmozgás egyenlete, amelyben a K állandó (2π/T)2-nel egyezik meg. Innen a rezgésidő:
T=2π√(R−d)2+R2−d2gd=2π√2R(R−d)gd=2,61 s.
II. megoldás. Tekintsük a kicsiny α0 szöggel kitérített és kezdősebesség nélkül elindított hiányos hengerpalástot. A kicsiny kezdeti kitérés miatt a test szögelfordulása időben így változik:
α(t)=α0cosΩt,
ahol Ω=2πT (T a keresett periódusidő). Ez az időfüggés minden olyan mozgásra igaz, ahol egy stabil egyensúlyi helyzetből mozdítottuk ki a testet, és a rá ható erők a kitérésnek ,,sima'' (differenciálható) függvényei.
A rezgőmozgás összefüggései szerint a hengerpalást legnagyobb szögsebessége (amikor áthalad az egyensúlyi helyzetén):
ωmax=α0Ω.
(Vigyázat: Ne tévesszük össze a rezgőmozgás Ω körfrekvenciáját a test ω szögsebességével!)
Írjuk fel a test összes mechanikai energiáját a legnagyobb kitérésű és a legnagyobb szögsebességű állapotára, és alkalmazzuk az energiamegmaradás törvényét (2. ábra):
mgd(1−cosα0)=mgd⋅2sin2(α0/2)≈mgdα202=12ΘPω2max=12ΘP(2πT)2α20,
vagyis
mgd=ΘP(2πT)2.
Ebben a képletben
ΘP=ΘT+m(R−d)2=ΘO+md2+m(R−d)2=2mR(R−d)
a testnek a talajjal érintkező P pontjára vonatkozó tehetetlenségi nyomatéka a szimmetrikus helyzetben, amint azt a Steiner-tétel kétszeri alkalmazása után kaphatjuk.

2. ábra
Az energiamegmaradás egyenletéből követketik, hogy a periódusidő
T=2π√2R(R−d)gd=2,61 s.
Statisztika:
19 dolgozat érkezett. 5 pontot kapott: Somlán Gellért, Téglás Panna, Toronyi András. 4 pontot kapott: Kertész Balázs, Ludányi Levente. 3 pontot kapott: 8 versenyző. 2 pontot kapott: 1 versenyző. 1 pontot kapott: 5 versenyző.
A KöMaL 2021. januári fizika feladatai
|
|

