A P. 5290. feladat (2021. január)

P. 5290. Homogén elektromos mező \(\displaystyle P\) pontjából egy pontszerű, negatív töltésű részecskét lövünk ki az elektromos térre merőleges \(\displaystyle \boldsymbol v_0\) kezdősebességgel. Az \(\displaystyle \boldsymbol E\) elektromos térerősségre és a \(\displaystyle \boldsymbol v_0\) sebességvektorra merőleges, homogén mágneses mező is jelen van. A kétféle mezőt egy, az elektromos térerősségre merőleges sík választja el egymástól az ábra szerint. Mekkora a mágneses indukcióvektor nagysága, ha a részecske visszatér a \(\displaystyle P\) pontba?

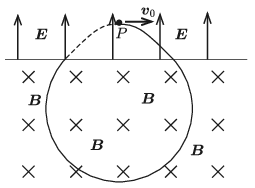
(Az egész elrendezés vákuumban van, és a nehézségi erő hatása a részecskére elhanyagolható.)

Közli: Németh László, Fonyód

(5 pont)

A beküldési határidő 2021. február 18-án LEJÁRT.

Megoldás. Jelöljük a részecske töltésének nagyságát (abszolút értékét) \(\displaystyle Q\)-val, a tömegét \(\displaystyle m\)-mel, és a kétféle mezőt elválasztó sík távolsága az indítási ponttól legyen \(\displaystyle d\) (lásd az ábrát).

A részecske az elektromos térben

\(\displaystyle a=\frac{EQ}{m}\)

gyorsulással mozog a mezőket elválasztó sík felé, és

\(\displaystyle t=\sqrt{\frac{2d}{a}}=\sqrt{\frac{2dm}{EQ}}\)

idő alatt teszi meg a \(\displaystyle d\) távolságot. Eközben \(\displaystyle \boldsymbol v_0\) irányában egyenletesen mozogva

\(\displaystyle \ell=v_0t=\sqrt{\frac{2dmv_0^2}{EQ}}\)

utat tesz meg. A határoló síkhoz érve a sebességének egyik komponense \(\displaystyle v_0\), a másik (az elektromos térrel ellentétes irányú) komponense

\(\displaystyle v_1=at=\sqrt{\frac{2dEQ}{m}},\)

a sebességvektor nagysága pedig

\(\displaystyle v=\sqrt{v_0^2+v_1^2}\)

lesz.

A mágneses térbe belépve (ahol az elektromos térerősség már nulla) a \(\displaystyle \boldsymbol B\) indukcióvektornak és a \(\displaystyle \boldsymbol v\) sebességvektornak megfelelő Lorentz-erő a hatására a részecske egyenletes körmozgást végez. A körpálya sugara a mozgásegyenletből kapható meg:

\(\displaystyle QBv=\frac{mv^2}{R}, \qquad \text{tehát}\qquad R=\frac{mv}{QB}.\)

Ha a kör középpontja éppen a \(\displaystyle P\) pont ,alatt'' helyezkedik el, akkor a pálya szimmetrikus görbe lesz, és a részecske visszajut a \(\displaystyle P\) pontba. Hasonló háromszögek oldalainak arányából

\(\displaystyle \frac{\ell}{R}=\frac{v_1}{v},\)

ahonnan a korábbi részeredmények felhasználásával kapjuk, hogy

\(\displaystyle B=\frac{mv}{QR}=\frac{mv_1}{\ell Q}= \frac{m}{Q}\frac{\sqrt{\displaystyle\frac{2dEQ}{m}}}{\sqrt{\displaystyle\frac{2dmv_0^2}{EQ}}}=\frac{E}{v_0}.\)

Ez a meglepően egyszerű végeredmény (ami nem függ a \(\displaystyle Q\), \(\displaystyle m\) és \(\displaystyle d\) mennyiségektől) így is felírható:

\(\displaystyle {\boldsymbol E}={\boldsymbol v_0}\times {\boldsymbol B}.\)

Statisztika:

38 dolgozat érkezett.
5 pontot kapott:	Antalóczy Szabolcs, Barna Benedek, Biebel Botond, Bonifert Balázs, Dobre Zsombor, Fekete András Albert, Fey Dávid, Gurzó József, Hauber Henrik, Horváth 999 Anikó, Horváth Antal, Kertész Balázs, Kozák Gergely, Kozaróczy Csaba, Köpenczei Csanád, Ludányi Levente, Magyar Gábor Balázs, Mihalik Bálint, Mócza Tamás István, Molnár 123 Barnabás, Molnár-Szabó Vilmos, Mozolai Bende Bruno, Páhán Anita Dalma, Sas 202 Mór, Schäffer Bálint, Selmi Bálint, Somlán Gellért, Toronyi András, Tóth Ábel, Török 111 László, Tuba Balázs, Varga Vázsony.
4 pontot kapott:	Bognár 171 András Károly, Fonyi Máté Sándor.
3 pontot kapott:	2 versenyző.
2 pontot kapott:	1 versenyző.
Nem versenyszerű:	1 dolgozat.

A KöMaL 2021. januári fizika feladatai