 |
A P. 5294. feladat (2021. február) |
P. 5294. Egy félhenger alakú vályú tengelye vízszintes. A vályú egyik vízszintes sugarának \(\displaystyle P\) felezőpontján át különböző hajlásszögű lejtőket fektetünk. Mekkora annak a lejtőnek a hajlásszöge, amelyen egy súrlódásmentesen lecsúszó piciny test leghamarabb éri el a vályú felületét?
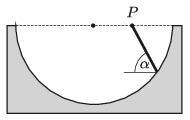
Közli: Holics László, Budapest
(5 pont)
A beküldési határidő 2021. március 16-án LEJÁRT.
Megoldás. A lejtőnek nyilván a vályú tengelyére merőleges, függőleges síkban kell feküdnie. A továbbiakban ezt a ,,síkbeli'' nézetet vizsgáljuk.
Ismert tétel, hogy egy adott \(\displaystyle P\) pontból induló, különböző hajlásszögű lejtőkön súrlódásmentesen lecsúszó testek bármelyik pillanatban egy olyan körön helyezkednek el, ami a \(\displaystyle P\) pontra illeszkedik, és a körnek a \(\displaystyle P\) ponthoz tartozó sugara függőleges. A kör sugara az eltelt idő négyzetével arányos, tehát a legrövidebb időnek az a kör felel meg, amelyik érinti vályú keresztmetszetének megfelelő félkört (1. ábra).
1. ábra
Jelöljük a vályú sugarát \(\displaystyle R\)-rel, a leggyorsabb lecsúszáshoz tartozó kör sugarát \(\displaystyle r\)-rel és a lejtőnek a függőlegessel bezárt szögét \(\displaystyle \varphi\)-vel (2. ábra).
2. ábra
Az \(\displaystyle OPA\) derékszögű háromszögre felírt Pitagorasz-tétel szerint
\(\displaystyle \left(\frac{R}{2}\right)^2+r^2=(R-r)^2,\)
vagyis
\(\displaystyle r=\frac{3}{8}R,\)
tehát
\(\displaystyle {\rm tg}\,2\varphi=\frac{R}{2r}=\frac{4}{3},\)
azaz
\(\displaystyle \varphi=26{,}6^\circ,\)
a lejtő hajlásszöge pedig
\(\displaystyle \alpha=90^\circ-\varphi=63{,}4^\circ.\)
Statisztika:
52 dolgozat érkezett. 5 pontot kapott: Barna Benedek, Berkesi Tímea, Biebel Botond, Bonifert Balázs, Dékány Csaba, Dóra Márton, Fekete András Albert, Gábriel Tamás, Gurzó József, Horváth 999 Anikó, Juhász Márk Hunor, Kertész Balázs, Köpenczei Csanád, Ludányi Levente, Mihalik Bálint, Mócza Tamás István, Molnár-Szabó Vilmos, Mozolai Bende Bruno, Németh Kristóf, Páhán Anita Dalma, Puskás Attila, Sallai Péter, Sándor Dominik, Selmi Bálint, Somlán Gellért, Szabó Márton, Téglás Panna, Toronyi András, Tóth Ábel. 4 pontot kapott: Antalóczy Szabolcs, Dózsa Levente, Fonyi Máté Sándor, Nemeskéri Dániel, Varga Vázsony. 3 pontot kapott: 2 versenyző. 2 pontot kapott: 3 versenyző. 1 pontot kapott: 6 versenyző. 0 pontot kapott: 7 versenyző.
A KöMaL 2021. februári fizika feladatai