 |
A P. 5297. feladat (2021. február) |
P. 5297. Egy könnyű, hajlékony, nyújthatatlan damilszál hossza \(\displaystyle \ell=80\) cm. A szál végeit azonos magasságban, egymástól valamekkora távolságban rögzítjük. A szálon egy \(\displaystyle m=5\) g tömegű, közepén átfúrt acélgolyó tud csúszni. Az acélgolyót olyan helyzetből indítjuk, aminél a feszes damilszál egyik része függőleges.
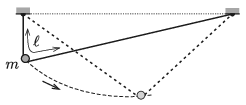
\(\displaystyle a)\) Legfeljebb mekkora sebességre gyorsul fel az acélgolyó, ha a súrlódás és a közegellenállás elhanyagolható?
\(\displaystyle b)\) Mekkora erő feszíti a damilt, amikor az acélgolyó sebessége maximális?
(Az acélgolyót tekintsük tömegpontnak!)
Holics László mérési feladata nyomán
(5 pont)
A beküldési határidő 2021. március 16-án LEJÁRT.
Megoldás. A golyó pályája (a damil hosszának állandósága miatt) egy olyan ellipszis, amelynek fél nagytengelye \(\displaystyle a= 40~\rm cm\) hosszúságú, és a fókuszpontjai a damilszál rögzítési pontjai. A fókuszpontok távolságát \(\displaystyle 2c\)-vel jelölve az ellipszis fél kistengelye \(\displaystyle b=\sqrt{a^2-c^2}\). A lecsúszó test sebessége akkor lesz a legnagyobb, amikor a kezdeti helyzetéhez képest a legnagyobb a függőleges irányú lesüllyedése. Ez a helyzet az ellipszis kistengelyének alsó végpontja.
\(\displaystyle a)\) Kezdetben az acélgolyó a nagytengely alatt, attól \(\displaystyle x \) távolságra van. Az ábrán látható derékszögű háromszögre felírt Pitagorasz-tételből leolvashatjuk, hogy
\(\displaystyle x^2+(2c)^2=(2a-x)^2,\)
innen
\(\displaystyle x=\frac{a^2-c^2}{a}=\frac{b^2}{a}.\)
A pálya legmélyebb pontjánál a test távolsága a nagytengelytől \(\displaystyle b\), tehát a munkatétel szerint
\(\displaystyle \frac{1}{2}mv_\text{max}^2=mg\left(b-\frac{b^2}{a}\right),\)
ahonnan
\(\displaystyle v_\text{max}=\sqrt{2g\left(b-\frac{b^2}{a}\right)}.\)
Mivel \(\displaystyle g\) és \(\displaystyle a\) adott nagyságú, a zárójelben álló, \(\displaystyle b\)-től kvadratikusan függő kifejezés akkor lesz a legnagyobb, amikor a \(\displaystyle b=a/2\). Innen már következik, hogy
\(\displaystyle v_\text{max}=\sqrt{\frac{ga}{2}}=1{,}4~\frac{\rm m}{\rm s}.\)
\(\displaystyle b)\) A kistengely végpontjánál az ellipszis görbületi sugara: \(\displaystyle R=a^2/b\), esetünkben \(\displaystyle R=2a\). Ha a damilt az acélgolyó legnagyobb sebességénél \(\displaystyle F\) erő feszíti, akkor a két oldalon ható erők eredője függőlegesen felfelé mutat, és a nagysága \(\displaystyle b=a/2\) miatt ugyancsak \(\displaystyle F\). A mozgásegyenlet szerint
\(\displaystyle F-mg=m\frac{v_\text{max}^2}{R},\)
ahonnan a keresett erő:
\(\displaystyle F=mg+m\frac{v_\text{max}^2}{R}=mg+m\frac{ga}{2\cdot 2a}=\frac 54 mg\approx 0{,}06~\rm N.\)
Statisztika:
41 dolgozat érkezett. 5 pontot kapott: Antalóczy Szabolcs, Bonifert Balázs, Fonyi Máté Sándor, Hauber Henrik, Kertész Balázs, Ludányi Levente, Mozolai Bende Bruno, Németh Kristóf, Sas 202 Mór, Selmi Bálint, Somlán Gellért, Téglás Panna, Toronyi András, Tóth Ábel, Varga Vázsony, Viczián Máté. 4 pontot kapott: Biebel Botond, Fekete András Albert, Gábriel Tamás, Köpenczei Csanád, Páhán Anita Dalma, Puskás Attila, Schmercz Blanka. 3 pontot kapott: 6 versenyző. 2 pontot kapott: 3 versenyző. 1 pontot kapott: 5 versenyző. 0 pontot kapott: 3 versenyző. Nem versenyszerű: 1 dolgozat.
A KöMaL 2021. februári fizika feladatai