 |
A P. 5298. feladat (2021. február) |
P. 5298. Két, egyenként \(\displaystyle m = 0{,}25\) kg tömegű, kis méretű acélgolyó \(\displaystyle \ell = 60\) cm hosszú, nyújthatatlan fonállal van összekötve. A két golyót úgy tartjuk, hogy összekötő fonaluk vízszintes egyenes és feszültségmentes. Egy adott pillanatban a két golyót egyszerre, lökésmentesen elengedjük. \(\displaystyle h = 1{,}8\) m esés után az egyik golyó egy kiálló merev kőpárkányba ütközik. Az ütközés abszolút rugalmas.
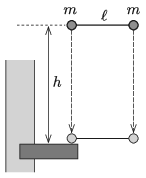
\(\displaystyle a)\) Mekkora erő feszíti a fonalat az ütközés utáni pillanatban?
\(\displaystyle b)\) Milyen magasságban lesz a párkányhoz képest az ütköző golyó az ütközés után \(\displaystyle t=\frac{1}{4}\) s múlva?
(A közegellenállás elhanyagolható.)
Közli: Holics László, Budapest
(4 pont)
A beküldési határidő 2021. március 16-án LEJÁRT.
Megoldás. \(\displaystyle a)\) Mindkét golyó \(\displaystyle v_0=\sqrt{2gh}\) sebességgel érkezik a párkány felső lapjának magasságába. Az ütközés utáni pillanatban a jobb oldali golyó \(\displaystyle v_0\) sebességgel mozog lefelé, az ütköző (bal oldali) golyó pedig \(\displaystyle v_0\) sebességgel felfelé. A rendszer tömegközéppontjának sebessége ekkor nulla. Mindkét golyó
\(\displaystyle \omega=\frac{v_0}{\ell/2}=\frac{\sqrt{4gh}}{\ell}\)
szögsebességgel kezd el keringeni a tömegközéppont körül, \(\displaystyle \ell/2\) sugarú körpályán. A fonalat feszítő erő
\(\displaystyle F=m\frac{\ell}{2}\omega^2= 8mg\,\frac {h}{\ell}\approx 29~\rm N.\)
\(\displaystyle b)\) A mozgás további részében a tömegközéppont szabadon esik lefelé, és a golyók állandó, \(\displaystyle \omega\) nagyságú szögsebességgel keringenek a tömegközéppont körül.
Az ütköző golyó elmozdulása az asztal lapjától lefelé:
\(\displaystyle x=\frac{g}{2}t^2-\frac{\ell}{2} \sin(\omega t)\approx 30{,}6~{\rm cm}-(-29{,}1~{\rm cm})\approx 60~{\rm cm}.\)
Negyed másodperc alatt körülbelül háromnegyed fordulatot tesz meg a rendszer.
Statisztika:
47 dolgozat érkezett. 4 pontot kapott: Albert Máté, Berkesi Tímea, Boda Benedek János, Csonka Illés, Dóra Márton, Fonyi Máté Sándor, Hauber Henrik, Horváth Antal, Kovács Kinga, Kozák Gergely, Köpenczei Csanád, Ludányi Levente, Mihalik Bálint, Mócza Tamás István, Nemeskéri Dániel, Perényi Barnabás, Puskás Attila, Selmi Bálint, Somlán Gellért, Szász Levente, Török 111 László. 3 pontot kapott: Bán Lőrinc Gábor, Beke Bálint, Bognár 171 András Károly, Brilli Fabiano, Dékány Csaba, Gábriel Tamás, Németh Kristóf, Schmercz Blanka, Strinyi Péter. 2 pontot kapott: 5 versenyző. 1 pontot kapott: 1 versenyző. 0 pontot kapott: 9 versenyző. Nem versenyszerű: 2 dolgozat.
A KöMaL 2021. februári fizika feladatai

