A P. 5302. feladat (2021. február)

P. 5302. Az ábrán látható alul zárt, $\displaystyle A$ keresztmetszetű, felül nyitott csövet függőleges helyzetben tartjuk úgy, hogy egy $\displaystyle m$ tömegű, benne könnyen csúszó, a csőből kissé kiérő tömör, nehéz dugattyút is fogunk.

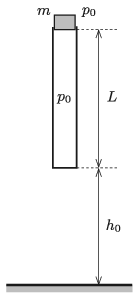
A külső $\displaystyle p_0$ légnyomás és a belső nyomás kezdetben megegyezik. A bezárt légoszlop kezdeti hossza $\displaystyle L$. A cső alja a vízszintes talajtól $\displaystyle h_0$ magasságra van. A külső és a kezdeti belső hőmérséklet $\displaystyle T_0$. Ezt a rendszert egy adott pillanatban kezdősebesség nélkül elengedjük. A cső alja az ütközéskor hozzátapad a talajhoz. (A csőben a súrlódás, valamint a külső légkörbeli közegellenállás elhanyagolható.)

$\displaystyle a)$ Mekkora lesz a maximális hőmérséklet a csőben?

$\displaystyle b)$ Mekkora lesz a dugattyú legnagyobb gyorsulása?

$\displaystyle c)$ Milyen magasra emelkedik a csőből kirepülő dugattyú?

Adatok: $\displaystyle A = 0{,}25~\mathrm{dm}^2$, $\displaystyle m = 0{,}5$ kg, $\displaystyle p_0 = 10^5$ Pa, $\displaystyle L = 0{,}8$ m, $\displaystyle h_0 = 0{,}6$ m, $\displaystyle T_0=300$ K.

Közli: Holics László, Budapest

(5 pont)

A beküldési határidő 2021. március 16-án LEJÁRT.

Megoldás. $\displaystyle a)$ A cső és a dugattyú az ütközés előtti pillanatban $\displaystyle v_0=\sqrt{2gh_0}$ sebességgel mozog. Az ütközéskor a cső hirtelen megáll, a dugattyú viszont $\displaystyle v_0$ kezdősebességgel mozog tovább. A csőben lévő levegő viszonylag gyorsan (nagyságrendileg tizedmásodperc alatt) nyomódik össze, a folyamat tehát tekinthető adiabatikusnak. Levegőre vonatkozó állapotegyenletek szerint

$\displaystyle pV^{1{,}4}=\text{állandó},\qquad\text{tehát}\qquad p\sim V^{-1{,}4}\qquad\text{és}\qquad T\sim pV\sim V^{-0{,}4}.$

Jelöljük a dugattyú pillanatnyi megállásához tartozó csőhosszat $\displaystyle xL$-lel ($\displaystyle x<1$), a levegő maximális nyomását $\displaystyle p$-vel, legmagasabb hőmérsékletét pedig $\displaystyle T$-vel. Az adiabatikus egyenletek szerint

$\displaystyle p=p_0\,x^{-1{,}4}, \qquad E=\frac{5}{2}pAL=\frac{5}{2}p_0AL\,x^{-0{,}4}\qquad \text{és}\qquad T=T_0x^{-0{,}4}.$

Írjuk fel az energiamegmaradás tételét az ütközés pillanatának és a dugattyú megállásának megfelelő állapotok között:

$\displaystyle \frac{1}{2}mv_0^2+mgL+\frac{5}{2}p_0AL+p_0AL(1-x)=mgxL+\frac{5}{2}p_0ALx^{-0{,}4}.$

(A bal oldal utolsó tagja a $\displaystyle p_0$ nyomású légkör által a gázon végzett munkával egyenlő.) A fenti egyenletből $\displaystyle v_0=\sqrt{2gh_0}$ felhasználásával algebrai átrendezés után ezt kapjuk:

$\displaystyle \frac{mg}{Ap_0}\cdot\frac{h_0}{L}+\left(\frac{mg}{Ap_0}+1\right)(1-x)=\frac52\left(x^{-0{,}4}-1\right).$

A megadott számadatok mellett

$\displaystyle \frac{mg}{Ap_0}=0{,}02 \qquad \text{és}\qquad \frac{h_0}{L}=0{,}75,$

így a megoldandó egyenlet

$\displaystyle 0{,}015+1{,}02\,(1-x)=2{,}5\,\left(x^{-0{,}4}-1\right).$

Ennek numerikus megoldása $\displaystyle x=0{,}85$, a keresett maximális hőmérséklet tehát

$\displaystyle T=\frac{T_0}{0{,}85^{ 0{,}4}}\approx 320~\rm K.$

Megjegyzés. A dugattyú $\displaystyle v_0\approx 3~$m/s sebességről $\displaystyle (1-x)L\approx 10$ cm út megtétele után áll meg. Ha egyenletesen lassult volna, akkor a megállásig kb. 0,1 s telt volna el. A változó gyorsulású mozgásnál is nagyságrendileg hasonló idő, tehát kb. tizedmásodperc telik csak el a dugattyú megállásáig. Ezalatt számottevő hőcsere nem alakul ki a dugattyú és a bezárt levegő között. Ez utólag megerősíti azt a feltevésünket, hogy a folyamat tekinthető adiabatikusnak.

$\displaystyle b)$ A szabadon eső csőben a dugattyú ,,súlytalan'', emiatt az ütközés pillanatában a csőben levő levegő nyomása még $\displaystyle p_0$. Amint a dugattyú belecsúszik a csőbe, a levegő nyomása megnő, tehát a dugattyú gyorsulása csökkenni kezd, valahol nullává válik, majd egyre nagyobb felfelé irányuló gyorsulásra tesz szert.

A legnagyobb gyorsulás a legnagyobb túlnyomás mellett alakul ki, vagyis amikor a dugattyú pillanatnyi sebessége éppen nulla. Ekkor a bezárt levelő nyomása:

$\displaystyle p_\text{max}=p_0 x^{-1{,}4}=1{,}255\,p_0.$

A dugattyú mozgásegyenlete ebben az állapotban:

$\displaystyle \left(p_\text{max}-p_0\right)A-mg=ma,$

ahonnan

$\displaystyle a=\left[(1{,}255-1)\left(\frac{p_0A}{mg}\right)-1\right]g=11{,}7\,g\approx115~\frac{\rm m}{\rm s^2}.$

$\displaystyle c)$ Az energiamegmaradás tétele szerint a felfelé mozgó dugattyú $\displaystyle v_0=\sqrt{2gh_0}$ nagyságú sebességgel éri el a cső tetejét, majd onnan további $\displaystyle h_0$ magasságra emelkedik. Ez éppen az a helyzet, ahonnan elejtettük. A dugattyú szempontjából az ütközés rugalmas (ha a súrlódásra és a közegellenállásra tett feltevések teljesülnek), csak a cső mechanikai energiája csökken le a rugalmatlan ütközés során.

Statisztika:

29 dolgozat érkezett.
5 pontot kapott:	Dóra Márton, Fonyi Máté Sándor, Kertész Balázs, Ludányi Levente, Németh Kristóf, Somlán Gellért, Téglás Panna, Toronyi András, Varga Vázsony.
4 pontot kapott:	Dékány Csaba, Schmercz Blanka.
3 pontot kapott:	2 versenyző.
2 pontot kapott:	6 versenyző.
1 pontot kapott:	6 versenyző.
0 pontot kapott:	4 versenyző.

A KöMaL 2021. februári fizika feladatai