A P. 5310. feladat (2021. március)

P. 5310. Szigetelt vezetőhuzalból egy olyan egyenlő oldalú háromszöget készítünk, amely a vízszintes \(\displaystyle OO'\) tengely körül súrlódásmentesen foroghat. A huzal merev, hosszegységre eső tömege \(\displaystyle \lambda\). Kezdetben a háromszög síkja függőleges, és olyan homogén mágneses mezőben van, amelyben a \(\displaystyle \boldsymbol B\) mágneses indukcióvektor függőlegesen felfelé mutat. Egy adott pillanatban feszültségforrást kapcsolunk a rendszerre, így abban \(\displaystyle I\) erősségű áram indul el. (Az induktivitástól eltekinthetünk.)

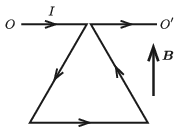
\(\displaystyle a)\) Mekkora gyorsulással indul el a háromszög vízszintes oldala?

\(\displaystyle b)\) Mekkora szöget zár be a háromszög síkja a függőleges iránnyal, ha elegendő ideig várunk?

Közli: Kotek László, Pécs

(5 pont)

A beküldési határidő 2021. április 15-én LEJÁRT.

Megoldás. Legyen a háromszög oldalainak hossza \(\displaystyle \ell\). Ekkor a drótkeret tömege \(\displaystyle 3\lambda\ell\), az \(\displaystyle OO'\) tengelyre vonatkoztatott tehetetlenségi nyomatéka pedig

\(\displaystyle \Theta= \lambda\,\ell \left(\frac{\sqrt{3}}{2}\ell\right)^2+\frac{\lambda\,\ell}{3} \left(\frac{\sqrt{3}}{2}\ell\right)^2 +\frac{\lambda\,\ell}{3} \left(\frac{\sqrt{3}}{2}\ell\right)^2=\frac{5}{4}\lambda\,\ell^3. \)

\(\displaystyle a)\) A \(\displaystyle T=\frac{\sqrt{3}}{4}\,\ell^2\) területű, \(\displaystyle I\) erősségű árammal átjárt drótháromszög mágneses dipólnyomatékának nagysága

\(\displaystyle \vert{\boldsymbol m}\vert=IT=\frac{\sqrt{3}}{4}I\ell^2.\)

Közvetlenül az áram bekapcsolása után \(\displaystyle {\boldsymbol m}\) vízszintes, így a drótháromszögre ható forgatónyomaték nagysága:

\(\displaystyle M=\vert {\boldsymbol m}\times {\boldsymbol B}\vert =\vert {\boldsymbol m}\vert\,B=\frac{\sqrt{3}}{4}BI \ell^2.\)

Ekkora forgatónyomaték hatására a drótkeret

\(\displaystyle \beta=\frac{M}{\Theta}=\frac{\sqrt{3}}{5}\,\frac{BI}{\lambda\ell}\)

szöggyorsulással indul el, tehát a vízszintes oldalának gyorsulása

\(\displaystyle a=\frac{\sqrt{3}}{2}\ell\,\beta=\frac{3}{10}\frac{BI}{\lambda}.\)

\(\displaystyle b)\) Elegendő hosszú idő alatt a drótkeret lengései lecsillapodnak. Egyensúlyi állapotban a mágneses mező forgatónyomatéka az \(\displaystyle OO'\) tengelyre ugyanakkora, mint a nehézségi erő forgatónyomatékának nagysága. A függőlegeshez képest \(\displaystyle \varphi\) szögkitérés esetén

\(\displaystyle \vert {\boldsymbol m}\times {\boldsymbol B}\vert=\vert {\boldsymbol m}\vert B\cos\varphi= \frac{\sqrt{3}}{4} I\ell^2B\cos\varphi=3\lambda\ell g\cdot \frac{2}{3}\frac{\sqrt{3}}{2}\ell\sin\varphi,\)

ahonnan

\(\displaystyle {\rm tg}\,\varphi=\frac14\,\frac{BI}{\lambda g}.\)

Statisztika:

29 dolgozat érkezett.
5 pontot kapott:	Biebel Botond, Kertész Balázs, Kozák Gergely, Ludányi Levente, Mozolai Bende Bruno, Puskás Attila, Selmi Bálint, Somlán Gellért, Téglás Panna, Toronyi András, Török 111 László.
4 pontot kapott:	Antalóczy Szabolcs, Bonifert Balázs, Fekete András Albert, Gurzó József, Hauber Henrik, Juhász Márk Hunor, Mócza Tamás István, Páhán Anita Dalma, Sas 202 Mór, Tóth Ábel, Varga Vázsony.
3 pontot kapott:	2 versenyző.
2 pontot kapott:	2 versenyző.
1 pontot kapott:	2 versenyző.
0 pontot kapott:	1 versenyző.

A KöMaL 2021. márciusi fizika feladatai