 |
A P. 5320. feladat (2021. április) |
P. 5320. Függőleges falból két azonos magasságban bevert szög áll ki, melyek távolsága L. A szögekre egy kötelet fektetünk úgy, hogy annak belógása H. Becsüljük meg a kötél teljes hosszát, ha tudjuk, hogy
a) H≪L;
b) L≪H.
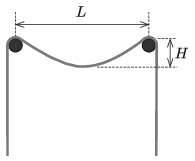
A súrlódás mindenütt elhanyagolható.
Közli: Berke Martin, Budapest
(5 pont)
A beküldési határidő 2021. május 17-én LEJÁRT.
Megoldás. a) A kötél belógó részét a szegeknél egy-egy F3 nagyságú, érintő irányú erő tartja, aminek vízszintes összetevője ±F1, föggőleges komponense pedig F2, ami éppen a belógó rész súlyának a fele. Jelöljük a kötél hosszegységre eső súlyát γ-val, a függőlegesen lelógó rész hosszát pedig X-szel (1. ábra).

1. ábra
a) Legyen H≪L. Ekkor a belógó kötél hossza jó közelítéssel L-nek vehető, így a súlya γL, és az egyensúlyának feltétele:
| (1) | 2F2=γL. |
A függőlegesen lelógó rész súlya γX, és ezt a kötéldarabot függőlegesen felfelé a kötél többi része F3 erővel húzza. Az erők egyensúlyának feltétele:
| (2) | F3=γX. |
Mivel H≪L, a két szög és a kötél felezőpontja majdnem egy egyenesbe esik, így a rájuk illeszkedő görbe jó közelítéssel parabola. A kötél érintőjének meredeksége a szög közvetlen közelében
tgα=F2F1,
ami a parabola ismert tulajdonsága szerint
tgα=4HL.
Fennáll tehát, hogy
| (3) | F2F1=4HL≪1, |
és így
| (4) | F3=√F21+F22≈F1. |
Az (1)-(4) összefüggések egybevetéséből kapjuk, hogy
X≈L28H,
így a kötél teljes hossza:
ℓ=2X+L=L24H(1+4HL)≈L24H.
b) L≪H esetén a belógó kötél mindkét fele majdnem függőleges (2. ábra), így X≈H, és a teljes kötélhossz
ℓ≈2X+2H≈4H.

2. ábra
Megjegyzés. Elég hosszú kötéllel mind az a), mind a b) helyzet megvalósítható. Mindkét helyzet instabil az aszimmetrikus változtatásokkal szemben, a szimmetrikus változtatások esetén az a) eset stabil, míg a b) eset instabil (a kötél vagy lecsúszik, vagy átmegy az a) helyzetbe).
Statisztika:
14 dolgozat érkezett. 5 pontot kapott: Dóra Márton, Gurzó József, Horváth 999 Anikó, Kertész Balázs, Ludányi Levente, Somlán Gellért, Téglás Panna, Tóth Ábel. 4 pontot kapott: Barna Benedek. 3 pontot kapott: 3 versenyző. 1 pontot kapott: 2 versenyző.
A KöMaL 2021. áprilisi fizika feladatai
|
|

