A P. 5321. feladat (2021. április)

P. 5321. Függőleges, alul zárt hengerekben lévő, különböző tömegű, súrlódásmentesen mozgó dugattyúk azonos térfogatú, azonos hőmérsékletű hélium-, illetve oxigéngázt zárnak el. A gázokat lassan azonos hőmérsékletre melegítjük fel. A melegítés során az oxigén belsőenergia 2,5-szer, a tágulási munkája pedig 220 J-lal nagyobb, mint a hélium esetében.

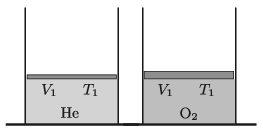
\(\displaystyle a)\) Határozzuk meg a gázok kezdeti nyomásának arányát!

\(\displaystyle b)\) Mennyit hőt közöltünk a melegítés során a héliummal, illetve az oxigénnel?

Közli: Kotek László, Pécs

(4 pont)

A beküldési határidő 2021. május 17-én LEJÁRT.

Megoldás. Legyen a hélium mólszáma \(\displaystyle n_1\), nyomása \(\displaystyle p_1\), az oxigénre ugyanezek \(\displaystyle n_2\) és \(\displaystyle p_2\). A gáztörvény szerint

\(\displaystyle p_1V_1=n_1RT_1, \qquad \text{illetve} \qquad p_2V_1=n_2RT_1,\)

ahonnan

\(\displaystyle \frac{p_1}{p_2}=\frac{n_1}{n_2}.\)

Melegítés során a gázok nyomása (a külső légnyomás és a dugattyú súlyából adódó nyomás összege) változatlan marad, így a megváltozott térfogatok aránya:

\(\displaystyle \frac{V_1'}{V_2'}=\frac{n_1}{n_2}\cdot \frac{p_2}{p_1}=1,\)

vagyis a megváltozott térfogatok is ugyanakkorák.

Legyen a térfogatváltozás (mindkét gázra) \(\displaystyle \Delta V\). A tágulási munka \(\displaystyle p\Delta V\), a belső energia megváltozása pedig \(\displaystyle \frac{f}{2}p\Delta V\) módon számítható ki. (Oxigénre \(\displaystyle f_2=5\), héliumra \(\displaystyle f_1=3\).) A megadott összefüggések szerint

\(\displaystyle p_2\Delta V-p_1\Delta V=220~{\rm J},\)

valamint

\(\displaystyle \frac{5}{2}\,p_2\Delta V=2{,}5\cdot \frac{3}{2}\,p_1\Delta V.\)

\(\displaystyle a)\) A fenti összefüggésekből következik, hogy a gázok nyomásának aránya:

\(\displaystyle \frac{p_1}{p_2}=\frac{2}{3},\)

továbbá

\(\displaystyle p_1\Delta V=440~{\rm J}\qquad \text{és}\qquad p_2\Delta V=660~{\rm J}.\)

\(\displaystyle b)\) Mindkét gáznál a vele közölt hő a belső energia megváltozásának és gáz által végzett munkának az összege. Héliumra ez

\(\displaystyle Q_1=\frac32\,p_1\Delta V+p_1\Delta V=\frac52 \,p_1\Delta V=1100~\rm J,\)

az oxigénre pedig

\(\displaystyle Q_2=\frac52\,p_2\Delta V+p_2\Delta V=\frac72 \,p_2\Delta V=2310~\rm J.\)

Statisztika:

40 dolgozat érkezett.
4 pontot kapott:	Bagu Bálint, Albert Máté, Antalóczy Szabolcs, Beke Bálint, Biebel Botond, Csonka Illés, Dóra Márton, Fekete András Albert, Gábriel Tamás, Hauber Henrik, Horváth 999 Anikó, Juhász Márk Hunor, Kertész Balázs, Kovács Kinga, Ludányi Levente, Mócza Tamás István, Mozolai Bende Bruno, Sas 202 Mór, Selmi Bálint, Somlán Gellért, Szabó Márton, Toronyi András.
3 pontot kapott:	Csapó Tamás, Hegymegi Balázs, Horváth Antal, Kaltenecker Balázs Bence, Kozák Gergely, Könye Sólyom, Perényi Barnabás, Puskás Attila, Schmercz Blanka, Strinyi Péter, Szász Levente, Téglás Panna, Török 111 László.
2 pontot kapott:	1 versenyző.
1 pontot kapott:	1 versenyző.
0 pontot kapott:	2 versenyző.
Nem versenyszerű:	1 dolgozat.

A KöMaL 2021. áprilisi fizika feladatai