A P. 5339. feladat (2021. szeptember)

P. 5339. Vízszintes, súrlódásmentes felületen egy $\displaystyle L = 0{,}6$ m hosszúságú, elhanyolható tömegű, vékony rúd fekszik. A rúd végpontjaihoz elhanyagolható tömegű, feszes fonalakkal $\displaystyle m = 0{,}2$ kg és $\displaystyle M = 0{,}8$ kg tömegű testeket rögzítettünk. A fonalak merőlegesek a rúdra. Egy adott pillanatban a rúd középpontjára a vízszintes felülettel párhuzamos, a rúdra merőleges, $\displaystyle F = 8$ N nagyságú erőt fejtünk ki.

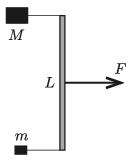
$\displaystyle a)$ Határozzuk meg a kezdőpillanatban a rúd középpontjának gyorsulását!

$\displaystyle b)$ A rúd melyik pontjára kellene kifejteni ezt az $\displaystyle F$ erőt, hogy a testek gyorsulása azonos legyen? Mekkora erők ébrednek ekkor a fonalakban?

Közli: Kotek László, Pécs

(4 pont)

A beküldési határidő 2021. október 15-én LEJÁRT.

Megoldás. $\displaystyle a)$ Jelöljük az $\displaystyle M$ tömegű testhez csatlakozó fonálban ható erőt $\displaystyle F_1$-gyel, a másikban ébredő erőt pedig $\displaystyle F_2$-vel. A rúd tömege és a tehetetlenségi nyomatéka elhanyagolható, ezért szükséges feltétel, hogy az erők összege és a forgatónyomatékok összege nulla legyen:

$\displaystyle F_1+F_2=8~{\rm N}\qquad\text{és}\qquad F_1\cdot (30~{\rm cm})-F_2\cdot (30~{\rm cm})=0.$

Ezek szerint

$\displaystyle F_1=F_2=4~\rm N.$

Az egyes testek gyorsulása:

$\displaystyle a_M=\frac{4~\rm N}{0{,}8~\rm kg}=5~{\rm m/s^2},\qquad a_m=\frac{4~\rm N}{0{,}2~\rm kg}=20~\rm m/s^2.$

A rúd középpontjának kezdeti gyorsulása a végpontok gyorsulásának számtani közepe, vagyis 12,5 m/s$\displaystyle ^2$.

$\displaystyle b)$ Ha a két test gyorsulása megegyezik, akkor a nagyobb tömegűre 4-szer akkora erő hat, mint a kisebb tömegűre:

$\displaystyle F_1=\frac{4}{5}F=6{,}4~{\rm N}, \qquad F_2=\frac{1}{5}F=1{,}6~{\rm N}.$

A forgatónyomatékok egyensúlya akkor teljesül, ha az $\displaystyle F$ erő hatásvonala a nagyobb tömegű testtől 12 cm távolságban, a kisebbtől 48 cm távolságban van.

Statisztika:

43 dolgozat érkezett.
4 pontot kapott:	Bencz Benedek, Czirók Tamás, Juhász-Molnár Erik, Kertész Balázs, Marozsi Lenke Sára, Somlán Gellért, Tárnok Ede , Vágó Botond, Waldhauser Miklós.
3 pontot kapott:	Kovács Kinga.
2 pontot kapott:	16 versenyző.
1 pontot kapott:	11 versenyző.
0 pontot kapott:	3 versenyző.

A KöMaL 2021. szeptemberi fizika feladatai