 |
A P. 5345. feladat (2021. szeptember) |
P. 5345. Vékony csőből két R sugarú negyedkört készítünk, majd egy-egy r sugarú, α szöggel ,,hiányos'' félkörívet csatlakoztatunk hozzájuk, végül az egész elrendezést az ábrán látható módon egy függőleges síklaphoz erősítjük. Az A pontból kezdősebesség nélkül beejtünk egy kis golyót a csőbe. A golyó az AB és a BC köríven végigcsúszik, a C és a D pont között szabadon esik (ferde hajítás szerint mozog), majd a DB és BE köríven csúszik tovább.(A súrlódást és a légellenállást figyelmen kívül hagyhatjuk.)
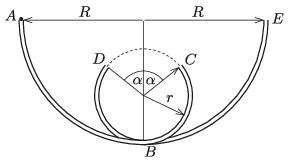
a) Mekkora az α szög, ha Rr=52?
b) Vizsgáljuk meg, hogy különböző Rr arányoknál mekkora α szög (vagy szögek) esetében valósulhat meg a leírt mozgás!
Romániai versenyfeladat nyomán
(6 pont)
A beküldési határidő 2021. október 15-én LEJÁRT.
Megoldás. Az energiamegmaradás tétele szerint a golyó sebessége a C pontban
v=√2g(R−r−rcosα),
amelynek függőleges és vízszintes komponense
vfelfelé=vsinα,vbalra=vcosα.
A golyó valamekkora t idő alatt eljut a D pontba, ahol a sebessége ugyancsak v lesz. Fennáll tehát, hogy
gt=2vfelfelé,
illetve
vbalrat=2rsinα.
(Feltehetjük, hogy α>0, tehát tényleges ferde hajításról van szó.) Ezekből az összefüggésekből t és v kiküszölése után ezt kapjuk:
cos2α−(Rr−1)cosα+12=0.
a) Amennyiben Rr=52, a fenti másodfokú egyenletből kapjuk, hogy cosα=0,5, azaz α=60∘.
b) Bevezetve a λ=R/r jelölést, az α szöget meghatározó egyenlet:
cos2α−(λ−1)cosα+12=0,
tehát
cosα=λ−1±√λ2−2λ−12.
A négyzetgyök alatt nem állhat negatív szám, vagyis λ=Rr≥1+√2≈2,41. A legkisebb arányhoz α=45∘-os szög tartozik.
A cosα-ra nézve másodfokú egyenletnek λ>1+√2 esetén két valós gyöke van. Az egyik gyök mindig kisebb 1-nél, a nagyobb gyök azonban λ>52 esetén 1-nél nagyobb, tehát számunkra érdektelen.
Összefoglalva: Ha 1+√2<Rr<52, akkor minden R/r arányszámhoz kétféle α is tartozhat. Rr>52, illetve Rr=1+√2 esetén csak egyetlen α szög mellett mehet végbe a mozgás, míg Rr<1+√2 esetén nincs olyan α szög, ami mellett a leírt mozgás megvalósulhatna.
Statisztika:
53 dolgozat érkezett. 6 pontot kapott: Antalóczy Szabolcs, Bencz Benedek, Biebel Botond, Fey Dávid, Hauber Henrik, Hegedűs Máté Miklós, Katona Attila Zoltán, Kertész Balázs, Kovács Márton András, Molnár Kristóf, Molnár-Szabó Vilmos, Mozolai Bende Bruno, Papp Marcell Imre, Schmercz Blanka, Seprődi Barnabás Bendegúz, Somlán Gellért, Téglás Panna, Toronyi András, Varga Mária Krisztina. 5 pontot kapott: Gábriel Tamás, Kürti Gergely, Veszprémi Rebeka Barbara. 4 pontot kapott: 9 versenyző. 3 pontot kapott: 13 versenyző. 2 pontot kapott: 5 versenyző. 1 pontot kapott: 1 versenyző. 0 pontot kapott: 2 versenyző.
A KöMaL 2021. szeptemberi fizika feladatai
|
|

