A P. 5365. feladat (2021. december)

P. 5365. Egy $\displaystyle \ell$ hosszúságú, $\displaystyle m$ tömegű, homogén, vékony rudat az egyik végpontjánál felfüggesztünk. Egyensúlyi helyzetéből kicsit kitérítve a lengéseinek periódusideje $\displaystyle T_0=2$ s, vagyis ez a rúd egy ,, másodpercinga''.

Tíz darab ugyanilyen rudat az ábrán látható módon erősítünk össze, majd a merev keretet az egyik csúcsánál fogva felakasztjuk. Az így kialakított ötágú csillag a saját síkjában szabadon elfordulhat az $\displaystyle O$ pont körül.

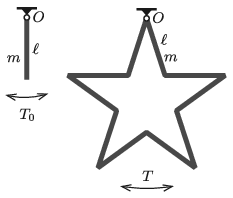
$\displaystyle a)$ Mekkora a rudak hossza?

$\displaystyle b)$ Mennyi az egyensúlyi helyzetéből kicsit kitérített ötágú csillag lengéseinek $\displaystyle T$ periódusideje?

(Lásd a sokszög alakú keretek lengéseiről szóló cikket lapunk 556. oldalán!)

Közli: Cserti József, Budapest

(5 pont)

A beküldési határidő 2022. január 17-én LEJÁRT.

I. megoldás. $\displaystyle a)$ A homogén rúd (mint fizikai inga) lengésideje:

$\displaystyle T_0=2\pi \sqrt{\frac{\frac13m\ell^2}{\frac12 mg\ell}}=2\pi\sqrt{\frac{2\ell }{3g}},$

ahonnan a rúd hossza:

$\displaystyle b)$ Az ötágú csillag tehetetlenségi nyomatékát először az $\displaystyle S$ súlypontra vonatkozóan számoljuk ki. Az $\displaystyle S$ pontból az egyes oldalak végpontjaiba mutató vektorok hosszára az 1. ábra alapján az alábbi egyenleteket írhatjuk:

$\displaystyle R \cos 2 \alpha = r \cos \alpha\qquad \text{és}\qquad r \sin \alpha = \ell\sin \beta,$

ahol $\displaystyle \alpha = \frac{360^\circ}{10}=36^\circ$ és $\displaystyle \beta = 90^\circ -2\alpha = 18 ^\circ$. Innen kapjuk, hogy

$\displaystyle R = \ell \, \mathrm{ctg}\,\alpha = 1{,}376\, \ell \qquad \text{és}\qquad r = \frac{\cos 2\alpha}{\sin \alpha} \,\ell = 0{,}526\, \ell.$

1. ábra

A hivatkozott cikk (4) képlete alapján a súlypontra vonatkoztatott tehetetlenségi nyomaték:

$\displaystyle \Theta_S = \frac{10 m}{6}\, \left(3 R^2 + 3 r^2-\ell^2 \right) = 0{,}919\, {M \ell^2},$

ahol $\displaystyle M= 10 m$ a csillag teljes tömege. A Steiner-tétel szerint a csillag teljes tehetetlenségi nyomatéka az $\displaystyle O$ pontra vonatkoztatva:

$\displaystyle \Theta = \Theta _S + M R^2 = 2{,}813 \, M \ell^2.$

Mivel a súlypont távolsága az $\displaystyle O$ ponttól $\displaystyle R$, így az $\displaystyle M$ tömegű csillag lengésének peridusideje:

$\displaystyle T = 2 \pi \, \sqrt{\frac{\Theta}{M g R}} = 8{,}98 \, \sqrt{\frac{\ell}{g}},$

azaz (1) felhasználásával

$\displaystyle T \approx 3{,}5~\rm s.$

II. megoldás. Az ötágú csillag tehetetlenségi nyomatékát más megfontolással is kiszámíthatjuk. Tekintsük a 2. ábrán vastag vonallal jelölt két rudat, és számítsuk ki a tehetetlenségi nyomatékukat a $\displaystyle T$ tömegközéppontjukra vonatkoztatva. (Használjuk az I. megoldás jelöléseit!)

2. ábra

Az ábrán $\displaystyle 2k\ell$-lel jelölt ,,hiányzó rész'' hossza

$\displaystyle 2k\ell=2\ell\sin 18^\circ, \qquad \text{vagyis}\qquad k=\sin 18^\circ=0{,}309.$

Egy-egy rúd tehetetlenségi nyomatéka a saját tömegközéppontjára $\displaystyle \frac{1}{12}m\ell^2,$ így a két rúdé a $\displaystyle T$ tömegközéppontra vonatkoztatva (a Steiner-tétel alkalmazásával):

$\displaystyle \Theta_T^\text{(két rúd)}=2\left(\frac{1}{12}+\left(k+\frac{1}{2}\right)^2 \right)m\ell^2=1{,}476\,m\ell^2.$

Az $\displaystyle S$ középpontra vonatkoztatva a két rúd tehetetlenségi nyomatéka (felhasználva, hogy $\displaystyle PT=d=\frac{\sin 18^\circ}{{\rm tg}\, 36^\circ}\ell=0{,}425\,\ell$)

$\displaystyle \Theta_P^\text{(két rúd)}=\Theta_T^\text{(két rúd)}+2md^2=1{,}837\,m\ell^2,$

a teljes csillagé pedig (ugyancsak $\displaystyle S$-re vonatkoztatva)

$\displaystyle \Theta_T^\text{(csillag)}=5\cdot \Theta_T^\text{(két rúd)}=9{,}186\,m\ell^2=0{,}919\,M\ell^2.$

(A megoldás további menete megegyezik az I. megoldáséval.)

Statisztika:

33 dolgozat érkezett.
5 pontot kapott:	Gábriel Tamás, Somlán Gellért, Téglás Panna, Toronyi András, Vig Zsófia.
4 pontot kapott:	Bubics Gergely Dániel, Dóra Márton, Hauber Henrik, Kertész Balázs, Kovács Kinga, Mészáros Ádám, Nemeskéri Dániel, Waldhauser Miklós.
3 pontot kapott:	10 versenyző.
2 pontot kapott:	5 versenyző.
0 pontot kapott:	2 versenyző.
Nem versenyszerű:	2 dolgozat.

A KöMaL 2021. decemberi fizika feladatai