A P. 5368. feladat (2021. december)

P. 5368. Egy $\displaystyle R=30$ cm sugarú, fémhuzalból készült karikának $\displaystyle Q=6\cdot10^{-6}$ C töltést adunk, majd a középpontján átmenő, a síkjára merőleges tengely körül $\displaystyle \omega=520$ 1/s szögsebességgel megforgatjuk vákuumban. Egy adott pillanatban egy elektron éppen a karika középpontján repül át $\displaystyle v=120$ m/s nagyságú, a karika síkjába eső sebességgel.

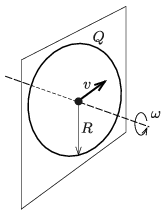
Mekkora az elektron pályájának görbületi sugara a karika középpontjában, ha ott a Föld mágneses tere éppen az elektron sebességének irányába mutat?

Közli: Holics László, Budapest

(5 pont)

A beküldési határidő 2022. január 17-én LEJÁRT.

Megoldás. Az összesen $\displaystyle Q$ nagyságú töltések $\displaystyle T=2\pi/\omega$ idő alatt tesznek meg egy fordulatot, és ez

$\displaystyle I=\frac{Q}{T}=\frac{Q\omega}{2\pi}=0{,}5~\rm mA$

erősségű áramnak felel meg.

Az $\displaystyle I$ erősségű áram által létrehozott mágneses indukcióvektor nagysága:

$\displaystyle B=\frac{\mu_0I}{2R}=1{,}0\cdot 10^{-9}~\rm T.$

A $\displaystyle v$ sebességű, $\displaystyle e$ töltésű elektronra tehát

$\displaystyle F=eBv=2\cdot 10^{-26}~\rm N$

nagyságú, a sebességére merőleges irányú erő hat. Ez az erő hozza létre az elektron centripetális gyorsulását:

$\displaystyle F=\frac{mv^2}{r},$

ahonnan a pálya görbületi sugara

$\displaystyle r=\frac{mv^2}F=0{,}66~\rm m.$

Megjegyzés. A forgó, töltött fémkarika által keltett mágneses tér sok nagyságrenddel gyengébb, mint a Föld mágneses terének nagysága az adott helyen. Esetünkben azonban az elektron sebessége éppen a földi mágneses tér indukcióvektorával párhuzamosan mozog, ezért a földi mágnesség járuléka a Lorentz-erőhöz nulla.

Statisztika:

25 dolgozat érkezett.
5 pontot kapott:	Bencz Benedek, Josepovits Gábor, Kertész Balázs, Kürti Gergely, Nemeskéri Dániel, Schmercz Blanka, Somlán Gellért, Téglás Panna, Toronyi András.
4 pontot kapott:	Beke Bálint, Buzási-Temesi Imre, Dobre Zsombor, Hauber Henrik, Magyar Gábor Balázs, Molnár 123 Barnabás, Vágó Botond.
3 pontot kapott:	2 versenyző.
2 pontot kapott:	1 versenyző.
1 pontot kapott:	1 versenyző.
0 pontot kapott:	1 versenyző.
Nem versenyszerű:	2 dolgozat.

A KöMaL 2021. decemberi fizika feladatai